zhuzilin's Blog
about
EOPL 读书笔记 Ch3
date: 2021-05-05
tags: PL
继续看 EOPL。
Ch3 Expression
本章主要学习变量的 binding 和 scoping。
3.1 Specification and Implementation Strategy
我们的 specification 会以如下的方式呈现:
(value-of exp ρ) = val我们的目标则是实现如下的工作流(图 3.1 a):
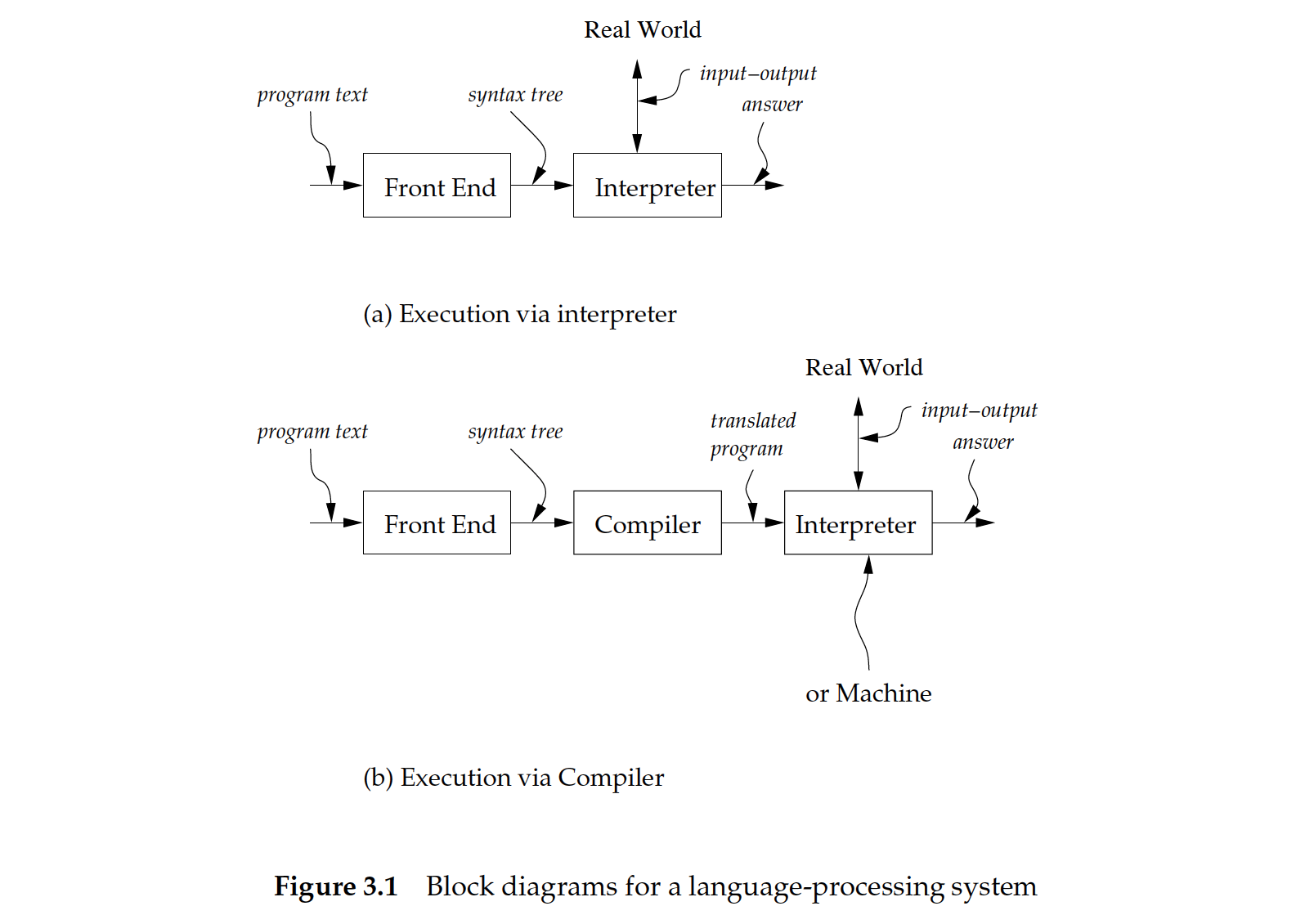
parsing 的部分主要有 2 个阶段,scanning 和 parsing,scanning 就是把字符串转化为 token 的过程;parsing 则是将 token 序列组织为具体的程序结构。一般会用 parser generator 来构建前端。
3.2 LET: A Simple Language
3.2.1 Specifying the Syntax
LET 的语法如下:
Program ::= Expression
a-program (exp1)
Expression ::= Number
const-exp (num)
Expression ::= -(Expression , Expression)
diff-exp (exp1 exp2)
Expression ::= zero? (Expression)
zero?-exp (exp1)
Expression ::= if Expression then Expression else Expression
if-exp (exp1 exp2 exp3)
Expression ::= Identifier
var-exp (var)
Expression ::= let Identifier = Expression in Expression
let-exp (var exp1 body)3.2.2 Specification of Values
每个语言都有 2 个集合:express value 和 denoted value,前者是表达式可能的值,后者是 values bound to variables。
对于本章的语言,express value 和 denoted value 一直相同,他们都是:
ExpVal = Int + Bool
DenVal = Int + BoolCh4 中会展现两者不太一样的语言。
为了利用上述定义,我们还加入了如下的 interface:
; constructor
num-val : Int → ExpVal
bool-val : Bool → ExpVal
; extractor
expval->num : ExpVal → Int
expval->bool : ExpVal → Bool这里我们认为 expval->num 和 expval->bool 可能是 undefined。
3.2.3 Environments
我们计划使用 2.2 中定义的 environment。enviroment 是一个函数,它的定义域是一个有限的变量集合,值域是 denoted value。我们还会使用如下的简写:
ρ表示环境[]表示空环境[var=val]ρ表示(extend-env var val ρ)[var1=val1, var2=val2]ρ相当于[var1=val1]([var2=val2]ρ)[var1=val1, var2=val2, ...]表示环境中var1的值为val1,var2为val2以此类推
3.2.4 Specifying the Behavior of Expressions
从上面的语法来看,LET 语言有 6 个 expression 和 1 个 observer:
# constructors:
const-exp : Int → Exp
zero?-exp : Exp → Exp
if-exp : Exp × Exp × Exp → Exp
diff-exp : Exp × Exp → Exp
var-exp : Var → Exp
let-exp : Var × Exp × Exp → Exp
# observer:
value-of : Exp × Env → ExpVal在实现语言之前,我们需要写下 specification for the behavior of these procedures:
; value of constant is constant
(value-of (const-exp n) ρ) = (num-val n)
; value of variable is determined by looking up the
; variable in the environment
(value-of (var-exp var) ρ) = (apply-env ρ var)
; value of a difference expression in some environment
; is the difference between the value of the first
; operand in that environment and the value of the
; second operand in that environment.
(value-of (diff-exp exp1 exp2) ρ)
= (num-val
(-
(expval->num (value-of exp1 ρ))
(expval->num (value-of exp2 ρ))))3.2.5 Specifying the Behavior of Programs
我们假设环境初始值为 [i=1, v=5, x=10],所以 program 的值为:
(value-of-program exp)
= (value-of exp [i=1,v=5,x=10])3.2.6 Specifying Conditionals
下一步就是要引入 boolean。LET 语言的 boolean constructor 是 zero?,它的 specification 为:
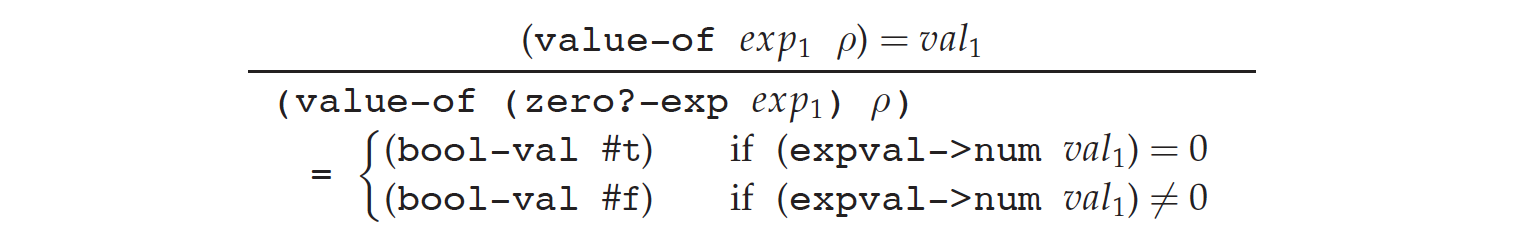
而 if 的 specification 为:
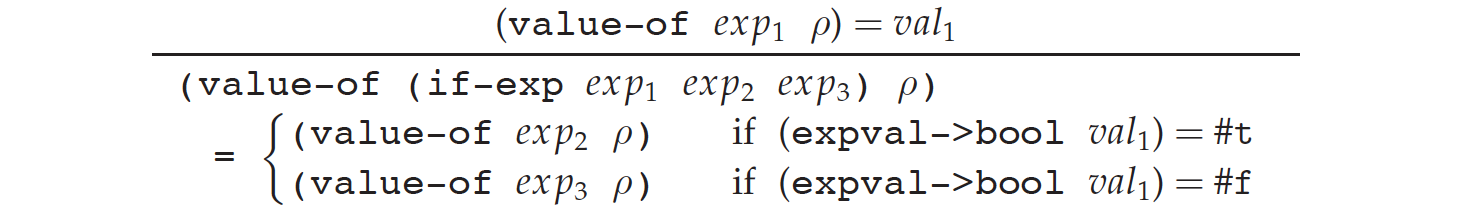
对于 if,equational specification 为:
(value-of (if-exp exp1 exp2 exp3) ρ)
= (if (expval->bool (value-of exp1 ρ))
(value-of exp2 ρ)
(value-of exp3 ρ))3.2.7 Specifying let
let 的变量类似于 lambda 的参数,是 bound 在 body 中的。
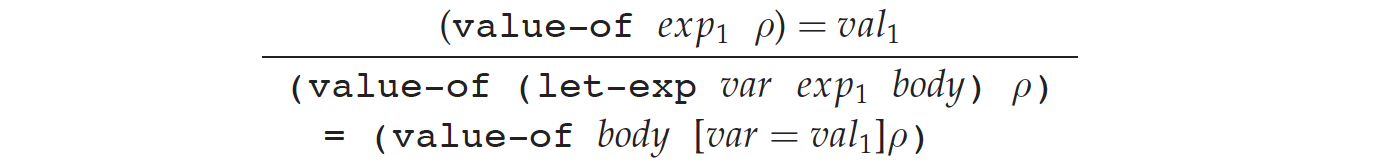
对应的等式为:
(value-of (let-exp var exp1 body) ρ)
= (value-of body [var=(value-of exp1 ρ)]ρ)3.2.8 Implementing the Specification of LET
至此,我们已经有了全部语法的 specification,接下来就是去实现它了。具体实现书中已经写了,就不抄下来了。
3.3 PROC: A Language with Procedure
PROC 语言里面加上了定义函数。所以 express value 和 denote value 就变成了:
ExpVal = Int + Bool + Proc
DenVal = Int + Bool + Proc还需要新加入创建以及调用函数的语法:
Expression ::= proc (Identifier) Expression
proc-exp (var body)
Expression ::= (Expression Expression)
call-exp (rator rand)由于加入了新的类型,所以我们需要新的 constructor procedure,用来创建函数和 extractor expval->proc,以及 observer apply-procedure,用来求值。并且我们会有以下的两个 specification:
(value-of (proc-exp var body) ρ)
= (proc-val (procedure var body ρ))
(value-of (call-exp rator rand) ρ)
= (let ((proc (expval->proc (value-of rator ρ)))
(arg (value-of rand ρ)))
(apply-procedure proc arg))最后,我们需要考虑 apply-procedure 是干啥用的:
(apply-procedure (procedure var body ρ) val)
= (value-of body [var=val]ρ)3.3.1 An Example
3.3.2 Representing Procedure
如何实现 Procedure,可以直接看书。大致使用 closure 实现的。
3.4 LETREC: A Language with Recursive Procedures
LETREC 让我们可以定义可以递归的函数。由于目前我们的函数只有一个参数,所以我们把 letrec 能定义的函数限定在单参数。有了这个语法,我们就可以实现这样的函数:
letrec double(x)
= if zero?(x) then 0 else -((double -(x,1)), -2)
in (double 6)为了这个功能,我们要添加这样的语法:
Expression ::= letrec Identifier (Identifier) = Expression in Expression
letrec-exp (p-name b-var p-body letrec-body)注意和 let 的区别在于 let 的等式左侧没有参数。
而 letrec 的等式则也会通过递归的方式更新环境:
(value-of
(letrec-exp proc-name bound-var proc-body letrec-body)
ρ)
= (value-of
letrec-body
(extend-env-rec proc-name bound-var proc-body ρ))上面这个等式相当于是把 letrec 做了啥这个问题转化为了 extend-env-rec 做了啥。因为 apply-env 是环境的唯一 observer,所以实际上我们只用考虑 (apply-env ρ1 var)(其中 ρ1 是 extend-env-rec 得到的环境)会返回什么就好了。
自然,我们要分类讨论:
-
当
var和proc-name相同,我们就可以直接取这个定义的函数。不过注意,在proc-body中仍然可能有proc-name出现,所以函数的 env 还得是ρ1:(apply-env ρ1 proc-name) = (proc-val (procedure bound-var proc-body ρ1)) -
当
var不是proc-name的时候,我们就可以忽略它:(apply-env ρ1 var) = (apply-env ρ var)
至此,我们就给出了 extend-env-rec 的 specification,根据他们,我们就可以实现 LETREC 了。
3.5 Scoping and Binding of Variables
在大多数编程语言中,变量以两种形式出现:reference 和 declaration。我们称:variable reference is bound by the declaration with which it is associated, and that it is bound to its value.
declaration 往往有 limited scope,从而让同一个变量名能够在不同地方担当不同的角色。决定每个 reference 指向哪个 declaration 的规则被称为 scoping rules。一个 declaration 保持 valid 的程序部分被称为该 declaration 的 scope。
我们称 inner declaration shadow 了 outer ones。
变量和值之间的联系关系称为 binding。对于我们实现的语言以及 scheme(Racket),每个 binding 的延续时间是不定长的,因为返回的值可能有闭包。我们称这种不定长为 semi-infinite extent。gc 只能在运行时判断一个 binding 是否不再 reachable,这种运行时才能决定的特性,我们称之为 dynamic property。
3.6 Eliminating Variable Names
每个 scope 被称为一个 contour,对于一个变量来说,相互交叉(重叠)的 contour 数量被称为其 lexical (or static) depth,该值一般以 0 为起始。例如:
(lambda (x)
((lambda (a)
(x a))
x))上式最后一行的 x 的 depth 为 0,第三行的 x 的 depth 为 1。利用这个值,我们就可以抛弃掉变量名,将上式表示为:
(nameless-lambda
((nameless-lambda
(#1 #0))
#0))这里 nameliss-lambda 声明了一个匿名变量,而变量由其 lexical depth 表示。这些值也 uniquely identifies the declaration to which is refers。这些数被称为 lexical address 或 de Bruijn indices。编译器会周期性计算每个 reference 的 lexical address,从而丢掉变量名。
这种表示方法可以 predict 特定的变量会在环境的哪个地方。例如:
let x = exp1
in let y = exp2
in -(x,y)对这个 expression 求值,化简到最后会变成:
(value-of
<<let x = exp1
in let y = exp2
in -(x,y)>>
ρ)
=
(value-of
<<-(x,y)>>
[y=val2][x=val1]ρ)在最后的环境中, y 的位置为 0,x 的位置为 1,和他们的 lexical depth 相对应。
3.7 Implementing Lexical Addressing
我们来考虑如何实现上一节提到的 lexical address analysis。
3.7.1 The Translator
作为一个 translator,我们首先要明确 source language 和 target language。target language 自然是包含 nameless-var-exp 和 nameless-let-exp 这样的东西,并去掉了 source language 中有的 var-exp 和 let-exp。所以我们要加入下面的这几条语法:
Expression ::= %lexref number
nameless-var-exp (num)
Expression ::= %let Expression in Expression
nameless-let-exp (exp1 body)
Expression ::= %lexproc Expression
nameless-proc-exp (body)对于我们要实现的 translation-of 函数,他需要当前的 scope 信息,也就是 context,所以需要有 2 个参数,expression 和一个 static environment。static environment 中会用变量的列表表示当前的 scope 信息,这个变量列表中的第一个元素会对应最内侧 scope 定义的变量。static environment 的实现如下:
; Senv = Listof(Sym)
; Lexaddr = N
; empty-senv : () → Senv
(define empty-senv
(lambda ()
’()))
;extend-senv : Var × Senv → Senv
(define extend-senv
(lambda (var senv)
(cons var senv)))
; apply-senv : Senv × Var → Lexaddr
(define apply-senv
(lambda (senv var)
(cond
((null? senv)
(report-unbound-var var))
((eqv? var (car senv))
0)
(else
(+ 1 (apply-senv (cdr senv) var))))))在实现过程中,实际上就是遍历并拷贝 AST,并做 3 处修改:
- 遇到
var-exp就换成nameless-var-exp,并用apply-senv得到正确的 lexical address; - 遇到
let-exp就换成nameless-let-exp,然后把表达式用原来的 senv 更新,并把 body 用(extend-senv var senv)更新。 - 遇到
proc-exp就换成nameless-proc-exp,然后把 body 用新 senv ((extend-senv var senv))更新。
3.7.2 The Nameless Interpreter
我们需要的是一个 nameless environment。由于我们可以直接根据 index 去取值了,我们就可以用 list 来表示 enviroment,并用 list_ref 来进行取值:
; nameless-environment? : SchemeVal → Bool
(define nameless-environment?
(lambda (x)
((list-of expval?) x)))
; empty-nameless-env : () → Nameless-env
(define empty-nameless-env
(lambda ()
’()))
; extend-nameless-env : ExpVal × Nameless-env → Nameless-env
(define extend-nameless-env
(lambda (val nameless-env)
(cons val nameless-env)))
; apply-nameless-env : Nameless-env × Lexaddr → ExpVal
(define apply-nameless-env
(lambda (nameless-env n)
(list-ref nameless-env n)))有了这个新的 environment,简单调整一下其他函数,就可以实现 nameless interpreter 了。
感悟
第二遍看 eopl 的 Ch3 和第一遍的感受上有明显的区别:第一遍的时候因为非常不熟悉 Racket,所以把重点放在了具体的实现上,实际上属于只见树木不见森林;第二遍的感觉就是,通过明确的逻辑推导,会很自然地写出语法的 specification,后面的实现就会变得非常 trivial。