zhuzilin's Blog
about
EOPL 读书笔记 Ch4
date: 2021-05-06
tags: PL
继续看 EOPL。
Ch4 State
4.1 Computational Effects
求值和产生 effect 的区别是什么呢?effect 是 global 的,整个计算都能观察到,并影响整个计算。
我们主要关心一个 effect:向某个内存位置赋值。
赋值和绑定的区别是什么呢?binding 是 local 的,但是赋值可能是全局的。
我们将把 memory 建模为从 location 到 storable values 的 finite map。一般来说 storable values 和 expressed values 是相同的。
表示 location 的数据结构称为 reference。reference 有时被称为 L-values,表示其往往出现在赋值语句的左边。类似地,expressed values 被称为 R-values。
在本章中,我们会考虑 2 种设计,explicit references 和 implicit references。
4.2 EXPLICIT_REFS: A Langauge with Explicit References
在 explicit references 中,我们会把 reference 作为一种新的 expressed value:
ExpVal = Int + Bool + Proc + Ref(ExpVal)
DenVal = ExpVal我们要加入 3 个新操作:
newref:分配新 location,并返回其 referencederef:返回 reference 指向的 location 里面存储的值setref:改变 reference 指向的 location 里面存储的值
一个 EXPLICIT_REFS 语言的例子如下:
let g = let counter = newref(0)
in proc (dummy)
begin
setref(counter, -(deref(counter), -1));
deref(counter)
end
in let a = (g 11)
in let b = (g 11)
in -(a,b)4.2.1 Store-Passing Specifications
store-passing specification 中 store 会作为 value-of 的显示输入,并作为输出的一部分:
(value-of exp1 ρ σ0) = (val1,σ1)根据这点,我们可以更新之前的 specification。
constant:
(value-of (const-exp n) ρ σ) = (n,σ)difference:
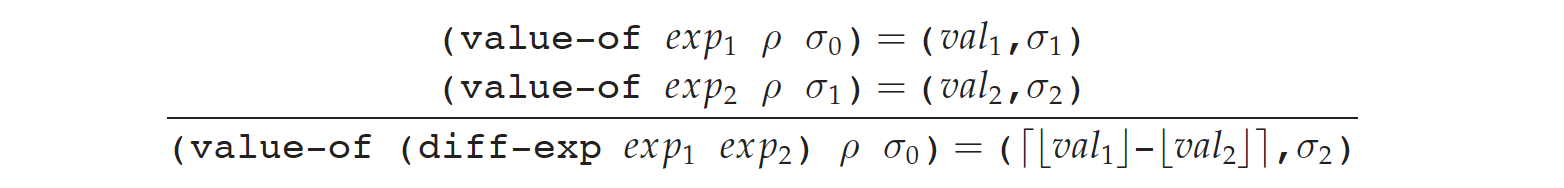
注意,假设中两次 value-of 的 store 都不一样。
if:
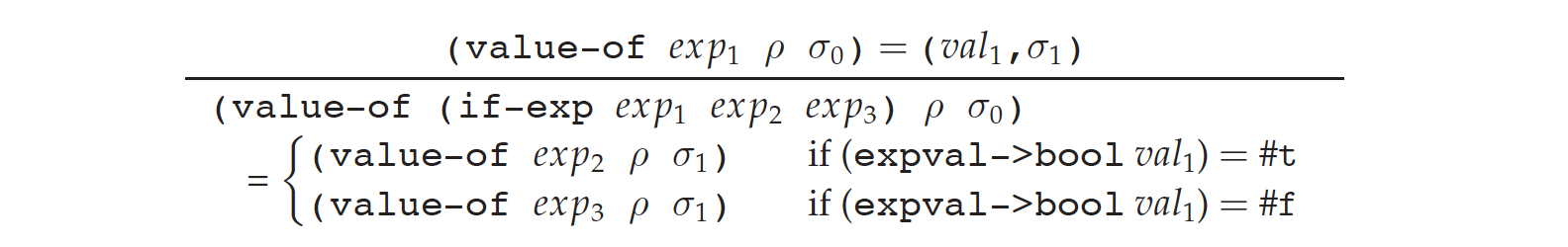
4.2.2 Specifying Operations on Explicit References
这一节我们来看一下 newref、deref 和 setref 的 specification。
首先是 newref:
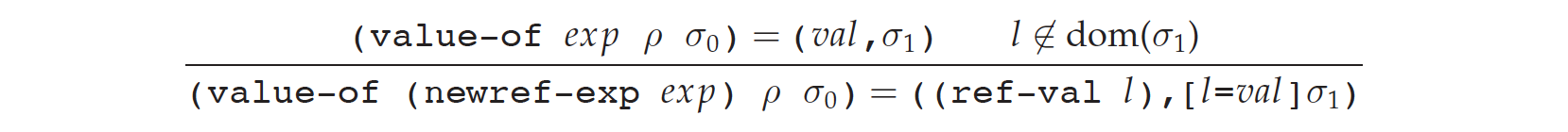
其次是 deref:
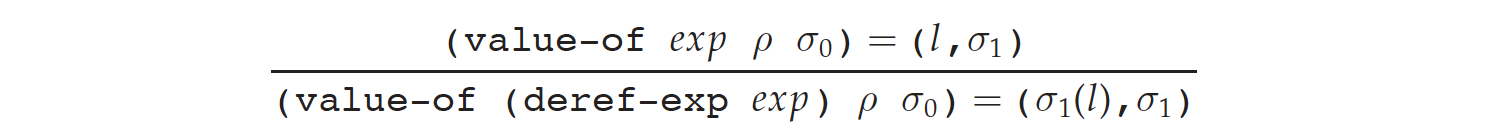
最后是 setref:
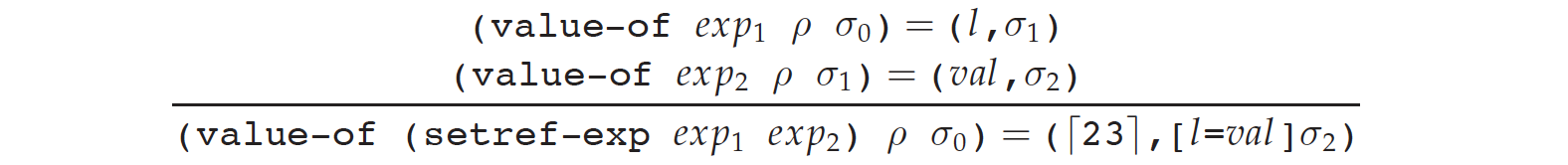
这里返回的 23 是个任意数。
4.2.3 Implementation
我们不打算如 specification 指示的去把 store 作为 value-of 的输入输出,而是打算使用 Scheme(Racket)本身的 store。为了简单起见,我们把 store 做成了一个 list,reference 就是 list 的位置。
; empty-store : () → Sto
(define empty-store
(lambda () ’()))
; usage: A Scheme variable containing the current state
; of the store. Initially set to a dummy value.
(define the-store ’uninitialized)
; get-store : () → Sto
(define get-store
(lambda () the-store))
; initialize-store! : () → Unspecified
; usage: (initialize-store!) sets the-store to the empty store
(define initialize-store!
(lambda ()
(set! the-store (empty-store))))
; reference? : SchemeVal → Bool
(define reference?
(lambda (v)
(integer? v)))从而得到了如下的实现:
; newref : ExpVal → Ref
(define newref
(lambda (val)
(let ((next-ref (length the-store)))
(set! the-store (append the-store (list val)))
next-ref)))
; deref : Ref → ExpVal
(define deref
(lambda (ref)
(list-ref the-store ref)))
; setref! : Ref × ExpVal → Unspecified
; usage: sets the-store to a state like the original, but with
; position ref containing val.
(define setref!
(lambda (ref val)
(set! the-store
(letrec
((setref-inner
; usage: returns a list like store1, except that
; position ref1 contains val.
(lambda (store1 ref1)
(cond
((null? store1)
(report-invalid-reference ref the-store))
((zero? ref1)
(cons val (cdr store1)))
(else
(cons
(car store1)
(setref-inner (cdr store1) (- ref1 1))))))))
(setref-inner the-store ref)))))直接看代码就好,还是挺清楚的。
4.3 IMPLICIT-REFS: A Language with Implicit References
很多语言把 reference 和 dereference 的过程隐藏起来了,也就是说所有的变量表示的都是 reference:
ExpVal = Int + Bool + Proc
DenVal = Ref(ExpVal)在每次 binding 的时候会创建 location,也就是每次的 procedure call, let 或 letrec。
当 variable 出现在 expression 中时,我们会查看 environment 来查看它 bound 的 location,之后查看 store 来找到值。也就是我们的 var-exp 是一个双层的系统。
location 中的值可以通过 set 表达式来改变,也就是新语法:
Expression ::= set Identifier = Expression
assign-exp (var exp1)这里的 Identifier 不是 expression 的一部分,所以不会被 dereference。
这种设计,我们称变量是可变的(mutable)。这种设计则被称为 call-by-value 或 implicit reference。大多数编程语言,包括 Scheme 在内,都采用了这种设计的某种变形。
let g = let count = 0
in proc (dummy)
begin
set count = -(count,-1);
count
end
in let a = (g 11)
in let b = (g 11)
in -(a,b)上面是 implicit reference 的一个例子,可以和上面的 explicit 的例子比较一下。
4.3.1 Specification
首先是取值:
(value-of (var-exp var) ρ σ) = (σ(ρ(var)), σ)然后是 assign,也就是 set:
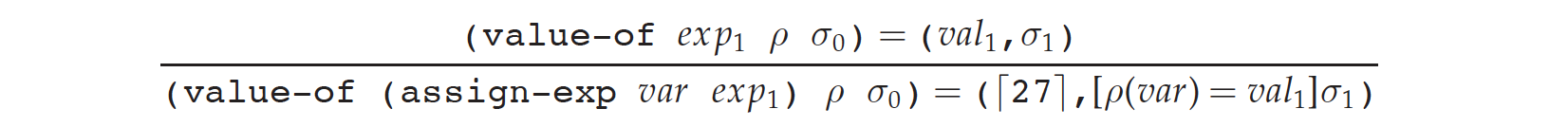
这里的 27 也是个随机数。
然后是 apply-procedure:
(apply-procedure (procedure var body ρ) val σ)
= (value-of body [var = l]ρ [l = val]σ)注意这里是没有垃圾回收的,每次调用都会使用新的 location。
4.3.2 Implementation
照着 specification 写就行。里面还是要用到 4.2 中定义的 newref,deref 和 setref! 的。
4.4 MUTABLE-PAIRS: A Language with Mutable Pairs
在练习 3.9 中,我们在语言中加入了 list,不过当时的 list 是不可变的(也就是没有 scheme 中的 set-car! 和 set-cdr!)。在这一节中,我们将给 IMPLICIT-REFS 中加上 mutable pairs。这样 expressed value 变成:
ExpVal = Int + Bool + Proc + MutPair
DenVal = Ref(ExpVal)
MutPair = Ref(ExpVal) × Ref(ExpVal)还有加入下列 interface:
newpair : Expval × Expval → MutPair
left : MutPair → Expval
right : MutPair → Expval
setleft : MutPair × Expval → Unspecified
setright : MutPair × Expval → Unspecified4.4.1 Implementation
4.4.2 Another Representation of Mutable Pairs
我们知道 MutPair 的两个值的存储位置相邻,所以实际上我们可以只用左边的元素的 reference 表示整体的 reference。
4.5 Parameter-Passing Variations
4.5.1 CALL-BY-REFERENCE
4.5.2 Lazy Evaluation: CALL-BY-NAME and CALL-BY-NEED
如果 body 不使用其参数,那么我们就不需要 evaluate 它。
letrec infinite-loop (x) = infinite-loop(-(x,-1))
in let f = proc (z) 11
in (f (infinite-loop 0))在上面这个例子中 infinite-loop 是不会停止的,但是在 lazy evaluation 的情况下,这个程序会直接返回 11,因为并不会 evalutate 参数的值。
下面让我们来把我们的语言改成 lazy evaluation 的。为了表明