【翻译】直观理解高等密码学

长文预警！本文是 Intuitive Advanced Cryptography 这篇文章的翻译。在现代/高等密码学中充斥魔法一般的结论和工具，想弄明白他们是在做什么的往往需要补充大量的数学知识。这篇文章的作者 Nguyen Thoi Minh Quan 就是希望通过不那么准确的叙述，让非科班出身的大家也可以领略到密码学的美妙之处。

注：

• 原文链接在这里：https://github.com/cryptosubtlety/intuitive-advanced-cryptography
• 为了更符合中文表述，可能会在一些地方进行意译。有些翻译的不准确的地方希望告诉我，我会加以改正的~

摘要

对于大多数软件工程师来说，零知识证明（zero-knowledge proof）、同态加密、承诺机制（commitment scheme）、盲签名（blind signature）、格密码学（lattice based cryptography）、安全多方计算（secure multi-party computation）、不经意传输（oblivious transfer）等高等密码学协议看起来美丽且近似于魔法。它们都以难理解著称。不幸的是，我在能够理解高等数学和正式的密码学证明之前就从 phd 项目退学了，这让我经常得想些方法来绕过它们带给我的挑战。本文就是想分享我的一些笔记，希望他们能帮你建立对这些精妙的密码学协议的直观理解。除此之外，作为一名安全工程师，我会从攻击者角度（attack oriented）来分析这些协议，从而绕过它们的密码学证明。

1. 引言

为了看懂这篇文章，你需要先看完这 4 本书：[1]、[2]、[3]、[4]。只是开个玩笑，别被吓跑了哈 :)

上一段虽然只是个玩笑，但是却或多或少有些真实。高等密码学协议都基于很多我并不完全理解的高等数学概念。为了跨过数学障碍，我们需要找到一个简单方法来解读与展示这些数学概念。本文在数学上的解读可能并不准确，只求能让我们能进一步理解复杂的密码学协议。同样，我们也会适当牺牲对协议描述的精确性，专注于对他们的直观理解。亲爱的数学家和密码学家们，请原谅我对真正的数学和密码学协议的误读 :)

在进入背景知识章节前还要提一点。仅仅明白数学是不足以理解密码学的。究其根本，密码学是安全的一部分，即设计密码学协议仅仅是一个开始，我们需要保证他们是安全的。在这方面，我们不会深挖密码学证明，而是采用攻击者的角度对协议进行分析。

2. 背景知识

2.1 群

群 $(G,+)$ 是一个集合 $G$，集合中任意两个元素之间都可以做 $+$ 运算。

如果你觉得有些抽象，那不妨想一下整数集。如果只考虑加法运算 $+$，忽略乘法运算 $\cdot$， $(\mathbb{Z}, +)$ 就是一个群。另一个例子是这样的：给定一个整数 $p$，考虑集合 $\mathbb{Z}_p=\{0,1,\dots,p-1\}$，群运算 $+$ 定义为 $\mod{p}$ 加法（先求和然后对 $p$ 取模），那么你就得到了有限群 $(\mathbb{Z}_p, +)$。这个群称为有限群是因为集合 $\mathbb{Z}_p$ 只有 $p$ 个元素，是有限的。有限群的元素个数称为群的阶（order），表示为 $|G|$。

我们来更详细地观察一下我们的群 $(\mathbb{Z}_p, +)$。$0$ 被称为群的单位元（identity），因为

$\forall x\in\mathbb{Z}_p:x+0=0+x=x$

注意到用 $1$ 和 $\mod{p}$ 加法操作能做到这样的事儿：

$\begin{aligned} &1=1\mod{p}\\ &1+1=2\mod{p}\\ &1+1+1=3\mod{p}\\ &\underbrace{1+\dots+1}_{p-1\text{ times}}=p-1\mod{p}\\ &\underbrace{1+\dots+1}_{p\text{ times}}=0\mod{p}\\ \end{aligned}$

我们注意到用 $1$ 和 $\mod{p}$ 加法可以生成 $\mathbb{Z}_p$ 中所有的元素。一个有这样特性（能用群运算生成集合中所有元素）的元素被称为生成元（generator）。

更具体地说，如果 $p=6$，$(\mathbb{Z}_6, +)$ 有 6 个元素 $\{0,1,2,3,4,5\}$。$1$ 可以生成 $(\mathbb{Z}_6, +)$ 中的所有元素，所以它是 $(\mathbb{Z}_6, +)$ 的生成元。那 $2$ 呢？我们有：$2,2+2=4\mod{6},2+2+2=0\mod{6}$，即 $2$ 只能生成 $\mathbb{Z}_6$ 中的 3 个元素：$\{0,2,4\}$，所以 $2$ 不是 $(\mathbb{Z}_6, +)$ 的生成元。如果我们只考虑集合 $\{0,2,4\}$，用 $\mod{6}$ 加法作为运算，它也是一个群。而且它是被更大的群 $(\mathbb{Z}_6, +)$ 包含的，所以 $(\{0,2,4\}, +\mod{6})$ 被称为 $(\mathbb{Z}_6, +)$ 的子群（subgroup）。拉格朗日定理告诉我们群的阶被其子群的阶整除。在我们的例子中，$(\{0,2,4\}, +\mod{6})$ 的阶是 3，能整除 $(\mathbb{Z}_6, +)$ 的阶 6.

在结束这一节之前，我们来介绍一个方便的表示形式。如果 $X$ 是群 $G$ 的一个元素，我们会用 $kX$ 来表示 $\underbrace{X+\dots+X}_{k\ times}$。最小的满足 $nX=0$ 的数被称为 $X$ 的阶（order）。在我们之前的例子里，在 $\mathbb{Z}_6$ 中，$1$ 的阶为 6，$2$ 的阶为 3，因为：

$\underbrace{1+\dots+1}_{6\ times}=0\mod{6}\qquad\underbrace{2+\dots+2}_{3\ times}=0\mod{6}$

总结一下，一方面，因为群是一个抽象的数学概念，可以把群想象成 $(\mathbb{Z}_p, +)$。另一方面，不要把自己的对群元素的印象局限于数字，群元素可以是任何东西，例如矩阵、多项式、曲线上的点。

2.2 域

域是一个集合 $F$，集合上有加法和乘法 2 个操作。你无时无刻不在和域打交道。实数集 $\mathbb{R}$、有理数集 $\mathbb{Q}$、复数集 $\mathbb{C}$ 配以常规的加法和乘法都是经典的域。

在密码学中，我们经常使用下述有限域：给定质数 $p$，集合 $\{0,1,\dots,p-1\}$ 配以 $\mod{p}$ 加法和乘法，就是一个有限域，表示为 $\mathbb{F}_p$。例如，有限域 $\mathbb{F}_5$ 有 5 个元素 $\{0,1,2,3,4\}$，它对应的操作如下：$2+4=1\mod{5}, 3*4=12=2\mod{5}$。最后，$\mathbb{F}_p$ 是 $\mathbb{F}_{p^k}$ 的一个特例，在实际应用中也经常使用 $k\le 1$ 的情况。

2.3 椭圆曲线

一个椭圆曲线 $E$ 是一个点的集合 $P(x, y)$ ，集合中的点的 $x,y$ 满足方程 $y^2=x^3+ax+b$，且 $x,y\in\mathbb{F}_p$，$p$ 为质数。例如，考虑如下的曲线：

$\begin{aligned} p&=17\\ a&=14\\ b&=4\\ y^2&=x^3+ax+b(E) \end{aligned}$

坐标 $x,y$ 定义在 $\mathbb{F}_{17}$ 上并满足方程 $y^2=x^3+14x+4\mod{17}$。点 $P(8, 13)$ 就是 $E$ 上的一个点，因为 $13^2=8^3+14*8+4\mod{17}$。

椭圆曲线的一个特殊的性质在于我们可以定义点之间的 $+$ 运算，即，给定 2 点 $P,Q\in E$，$P+Q$ 是有效的，并且其结果是 $E$ 上的另一点 $R$。我们不关心这里的 $+$ 是怎么定义的，只需要知道 $(E, +)$ 是一个群。在实际操作中，我们不会直接和 $(E, +)$ 打交道，而是选一个基点（base point）$G$，并使用 $G$ 生成的子群，即群 $(\{0, G, \dots, (q-1)G\})$，这里 $q$ 是 $G$ 的阶。利用拉格朗日定理，有 $|G|$ 整除 $|E|$。我们称 $|E|/|G|$ 为辅因子（cofactor）。辅因子的值在密码学协议中扮演者重要的角色。

为什么密码学中广泛使用椭圆曲线呢？从数学角度来看，原因是椭圆曲线的点形成了群，有很好的的数学性质。但是有群结构并不足以在密码学上有用。从安全角度来看，椭圆曲线很流行是因为离散对数问题非常难，即给定点 $X$，基点 $G$，很难找到 $x$ 使得 $X=xG$，我们一般把这里的 $x$ 写作 $\log_G{X}$。

2.4 多项式模

我猜你已经对多项式很熟悉了。例如，$P(x)$ 是一个在 $\mathbb{F}_q$ 上的 $k$ 阶多项式，即 $P(x)=a_{k-1}x^k+a_{k-2}x^{k-2}+\dots +a_0$，其中 $a_0,\dots,a_{k-1}\in\mathbb{F}_q$。$\mod{n}$（$n$ 是个数字）也是一个熟悉的运算。那么把他们结合到一起是什么样的呢，也就是 $\mod{P(x)}$ 运算是什么样的呢？

最好来看看具体的例子。假设 $P(x)=x^5+x=1$。那么 $\mod{x^5+x+1}$ 长啥样呢？我们回头看一下 $\mod{7}$ 是啥意思。在 $\mod{7}$ 中，$7$ 等于 $0$。例如 $8+4=7+1+4=1+4=5 \mod{7}$。同样，在 $\mod{x^5+x+1}$ 的世界里，$x^5+x+1$ 等于 $0$，所以你可以把 $x^5+x+1$ 换成 $0$，或者把 $x^5$ 替换成 $-x-1$。再举个例子，$P_1(x)=x^4$，$P_2(x)=x^6+1$，如果我们分别求他们的和与乘积，并 $\mod{x^5+x+1}$，会得到：

$\begin{aligned} &P_2(x)=x^6+1=x*(x^5)+1=x*(-x-1)+1=-x^2-x+1\\ &P_1(x) + P_2(x)=x^4-x^2-x+1\\ &P_1(x)*P_2(x)=x^4*(-x^2-x+1)=-x^6-x^5+x^4\\ &=-x*x^5-(-x-x)+x^4=-x*(-x-1)+x+1+x^4=x^4+x^2+2x+1 \end{aligned}$

在本文中，我们会用 $\mathbb{Z}_q[x]/(P(x))$ 里的多项式，也就是多项式的系数在 $\mathbb{Z}_q$ 中，并且所有运算都要 $\mod{P(x)}$。

2.5 Alice、Bob 和 Eve

在密码学协议中，经常会提到 3 个角色：Alice、Bob 和 Eve。一般来说，Alice 想和 Bob 交流，而 Eve 想攻击 Alice、Bob 以及他们的交流过程。一个不那么显然的问题在于 Alice 和 Bob 是否可以相互信任。密码学实现中的常见错误就是认为 Alice 和 Bob 相互信任。一般把 Alice 或 Bob 可看作是带有恶意的会更好，即，Alice 和 Bob 都需要在交流的过程中注意保护自己。人生不易呀。等一下，是说我们谁都不应该相信吗？我可没这么说，不过你怎么理解都行 :)

注意，在实践中 Alice、Bob 和 Eve 都不是人，而是计算机程序。所以在我提到 Alice 的内存、Alice 的状态、Alice 的程序的时候不要惊讶。

2.6 量子计算机

在传统的计算机中，基本单元是比特，它的取值在任何时候都只能是 0 或 1。在量子计算机中，基本单元是量子比特，它可以同时处于 0 或 1。这使得量子计算机相较传统计算机计算能力更强。我们的量子计算机部分就结束了。你可能会奇怪为啥这一节这么短。如果我都能理解量子计算机了，我也就不会在这儿写直观理解密码学协议的文章了 :)

从密码学角度来说，之所以我们需要关心量子计算机，是因为 Peter Shor [5] 告诉我们量子计算机可以解决离散对数问题和整数分解问题，即，它可以破解大多数公钥算法。我没说量子计算机可以破解对称加密或 AES 对吧？是的，量子计算机无法破解 AES。目前仅有的量子攻击是使用 Grover 的量子搜索算法 [6]，这个算法可以在 $\sqrt{N}$ 的时间内搜索 $N$ 项。因此，如果你担心量子计算机可以破解你的对称加密，那么把你的 AES 钥匙从 128 位提到 256 位就好了。不要在那些试图推销量子安全对称加密的骗子身上花钱哦。

3. 椭圆曲线 Die-Hellman (ECDH) 密钥交换

如果 Alice 想和 Bob 用一种安全的方式交流，让偷听的 Eve 不知道他们俩在说啥，该怎么做呢？很简单，Alice 把自己的信息加密一下然后把密文发给 Bob 就好了。等等，你说 Alice 会加密信息，但是她用的是什么密钥呢？Alice 之前是怎么把自己的密钥发给 Bob 的呢？记住 Eve 一直都在偷听。这是不是听起来挺难的？的确，这是个困难的问题。不过幸运的是，Diffie 和 Hellman 发明了一个优雅的协议从而从本质上改变了密码学。

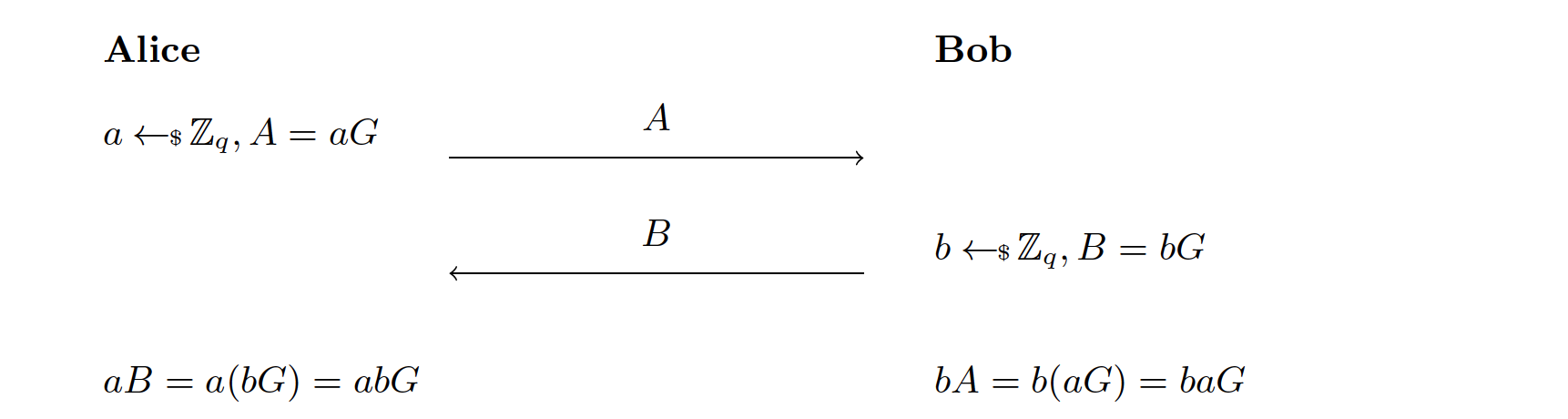
让我们说 Alice 和 Bob 事先同意使用一个常规的椭圆曲线 $E$，以及阶为 $q$ 的基点 $G$。Alice 生成一个随机私钥 $a\leftarrow_\$ \mathbb{Z}_q$，计算她的公钥 $A=aG$ 并发送给 Bob。Bob 生成随机私钥 $b\leftarrow_\$\mathbb{Z}_q$ 并计算出他的公钥 $B=bG$ 发送给 Alice。下面 Alice 计算 $aB=a(bG)=abG$，Bob 计算 $bA=b(aG)=baG$。注意到 Alice 和 Bob 计算出了相同的 $abG$，这个值可以作为他们的共享密钥用于后续的加密。

好啦，数学上是对的。下一步就是要说服自己这个协议是安全的。Eve 能知道什么呢？通过偷听 Alice 和 Bob，Eve 会知道 $A$（即 $aG$）、$B$（即 $bG$）。因为椭圆曲线的离散对数问题很难解，所以知道 $aG$ 和 $bG$ 不足以找到 $a$ 和 $b$，也就不能计算出 $abG$。所以共享密钥 $abG$ 是安全的。不过这个推断中有个漏洞。Eve 的目标是在已知 $aG$ 和 $bG$ 的情况下计算出 $abG$。在我的论据中，我假设她需要先计算出 $a,b$（即求解离散对数问题）才能计算 $abG$。但实际上有可能存在别的方法来计算 $abG$。因此，严格地说，我们需要设计一个新的安全性假设来保证这个协议是正确的。这被称为 Computational Diffie-Hellman（CDH）假设：给定 $G,aG,bG$，是几乎无法计算出 $abG$ 的。密码学是不是很微妙？一个很相近的问题是 Decisional Diffie-Hellman（DDH）：给定 $G,aG,bG$，几乎无法区分 $abG$ 和 $E$ 上的随机点。

3.1 主动攻击者和经过验证的密钥交换

在上一节中，我们假设 Eve 只偷听交流，也就是认为 Eve 是被动的。那么如果 Eve 主动干预 Alice 和 Bob 之间的交流会怎么样呢？

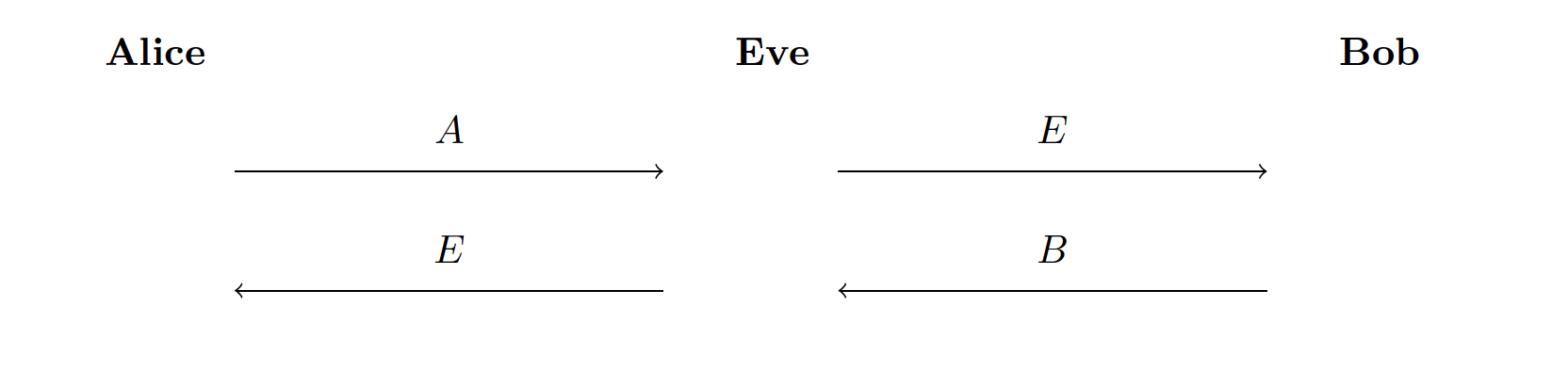
攻击的内容是，相较于直接把 Alice 的公钥 $A$ 传给 Bob，Eve 把自己的公钥 $E$ 发给 Bob。同样，Eve 把自己的公钥 $E$ 而不是 Bob 的公钥 $B$ 发给 Alice。最后 Eve 和 Alice 建立了共享密钥 $aeG$，和 Bob 建立了共享密钥 $beG$，从而可以解密 Alice 或 Bob 发送的任何密文。这里最本质的问题在于 Alice（Bob）接收到了他方发送过来的公钥，但是她（他）不知道这个公钥是来自 Bob（Alice）的。

为了避免这样的攻击发生，Alice 和 Bob 使用数字签名来处理他们的 ECHD 公钥 $A$ 与 $B$。因为 Eve 没法替 Alice 或 Bob 生成有效签名，上述的攻击就不奏效了。

3.2 ElGamal 加密

ECDH 密钥交换的一个直接的应用是 ElGamal 加密 [8,9]。基本的想法是用 ECDH 来建立共享密钥然后用共享密钥来遮盖信息。

为了加密消息 $m$，我们在 $E$ 上取点 $P_m$，它的 $x$ 坐标为 $m$。当 Bob 收到 Alice 的公钥 $A$ 之后，相较于 ECDH 中直接发送自己的公钥 $B$ 给 Alice，它会发送 $B$ 以及 $bA + P_m$ 给 Alice，即，$(c_1,c_2)=(B,bA+P_m)$，当 Alice 接收到 $(c_1,c_2)$ 时，她会计算 $c_2-ac_1=bA+P_m-aB=baG+P_m-abG=P_m$，而 $m$ 就是 $P_m$ 的 $x$ 坐标。

4 交互式零知识证明

你听说过零知识证明（zero-knowledge proof）吗？没有？你肯定不看新闻吧？零知识证明算是密码学协议中的热词了，难道你从来没听说过吗？我不是在问你知道不知道它是什么，只是想问问你有没有听说过它 :)

不正式地说，零知识证明是指在不透露某样东西的前提下，向别人证明你知道这样东西。听起来是不是像魔法一般？它的确就是魔法。零知识证明背后的技术是很复杂的，所以我们会拿一个具体的协议来进行分析。本节中的所有协议都需要参与各方之间的交互，所以这阶被称为交互式零知识证明。

4.1 Schnorr ID 协议

本节中，我们来分析一下 Schnorr ID 协议（Schnorr identification protocol）[10]。这是一个用作数字签名基础的很酷的协议，所以要集中注意力呀。

假设有椭圆曲线 $E$，其上有阶为 $q$ 的基点 $G$，Alice 的私钥为 $x$，她的公钥为 $X=xG$。Alice 想要在不把 $x$ 告诉 Bob 的前提下向 Bob 证明她知道 $x$。设计一个不暴露 $x$ 的协议很简单：Alice 什么都不做就行。设计一个 Alice 能说服 Bob 的协议甚至更简单：Alice 直接把 $x$ 发给 Bob 就好了。难的在于如何同时满足这两点。Schnorr [10] 发明了如下的协议：

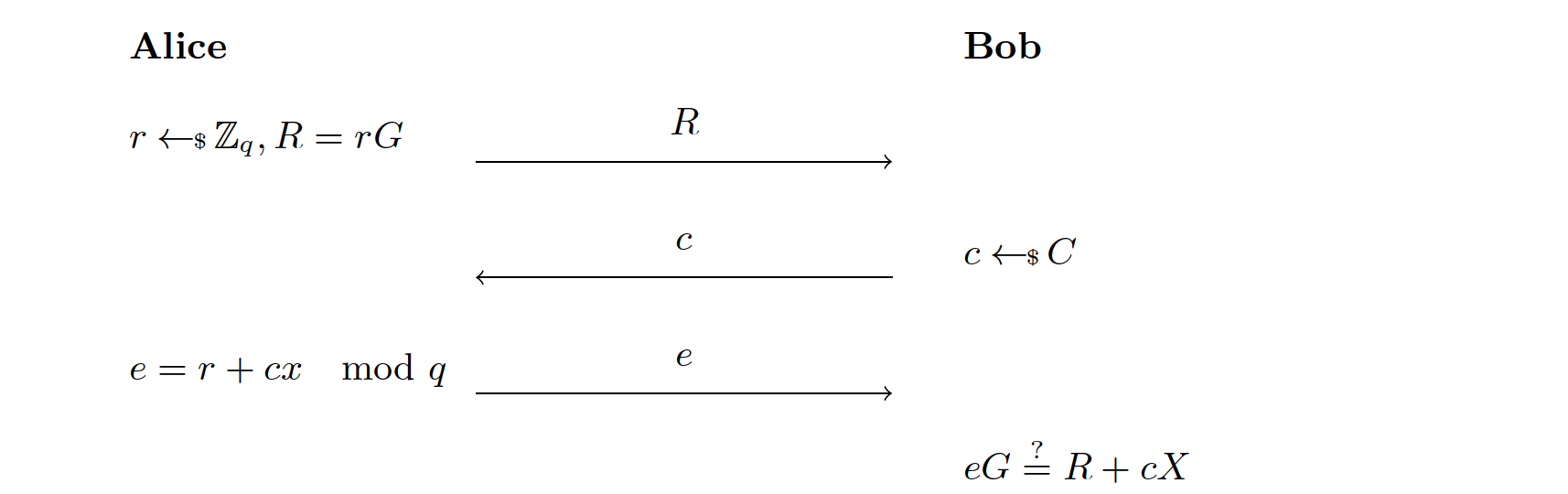
在上图中，$C$ 被称为挑战空间（challenge space），$c$ 是从 $C$ 中随机生成的（$c\leftarrow_{\$} C$）。在协议的最后，Bob 会验证 $eG$ 是否等于 $R+cX$。如果的确等于，那么 Bob 就相信 Alice 的确知道 $x$。注意如果 Alice 是诚实的，即 $e$ 的确等于 $r + cx$，那么把等式 $e=r+cx$ 两边都乘上 $G$，就有 $eG=rG+cxG=R+cX$。

为什么 Bob 对 $x$ 一无所知呢？他知道的和 $x$ 相关的仅有的信息是 $c=r+cx\mod{q}$，不管 $x$ 或 $cx$ 是啥，一个随机数 $r \mod{q}$ 都让结果和随机数无异，即 $r$ 完全遮盖了 $cx$ 的值。

另一个问题是为什么 $c$ 需要是不可预测的呢？如果 Alice 可以预测 $c$，那么她可以生成一个随机值 $e$，并计算 $eG$，使得 $R=eG-cX$，即，她可以在不知道 $r$ 和 $x$ 的情况下生成 $R$ 和 $e$，而 Bob 的验证却能通过。

好了，我们已经确信这个协议不会泄露 $x$ 了。那么剩下的难点在于 Bob 为什么会确信 Alice 知道 $x$。如果 Alice 不知道 $x$，那么不管我们对 Alice 做什么，我们都无法得到 $x$。如果允许我们控制并操纵 Alice 的运行环境，并且能从中得到 $x$，那么 Alice 肯定就知道 $x$（不然，$x$ 从哪儿来的呢？）你晕了吗？没事儿，我曾经比现在的你还晕 :) 对于这个协议，我们需要等到 Alice 生成 $r$ 和 $R=rG$ 之后克隆 Alice，即生成 2 个 Alice，她们有相同的 $r$。其中一个 Alice 收到 $c$，并发送 $e$，另一个 Alice 收到 $c'$，并发送 $e'$。我们有 $eG=R+cX,e'G=R+c'X\rightarrow (e'-e)G=(c'-c)X\rightarrow (e'-e)/(c'-c)G=X$，从而得到 $x=(e'-e)/(c'-c)$。一个很显然的问题是 Bob 是不是可以用类似的方法得到 $x$。如果 Bob 要得到 $x$，就需要保证 2 个 Alice 生成的是相同的 $r$。理论上的 Bob 是没有这个能力的。但是实际上，如果你的多线程 Alice 实现的不够仔细，就可能会受到这种攻击。别说我没警告过你 :)

4.2 Chaum-Pedersen 协议

取椭圆曲线 $E$，并假设 Alice 的私钥为 $x$。令 $G$ 和 $H$ 是 $E$ 上的两个点，Alice 会公开 $U=xG,V=xH$ 两个点。她想说服 Bob $\log_G{(U)}=\log_H{(V)}$，并在不透露 $x$ 的前提下证明她知道 $x$。[11]

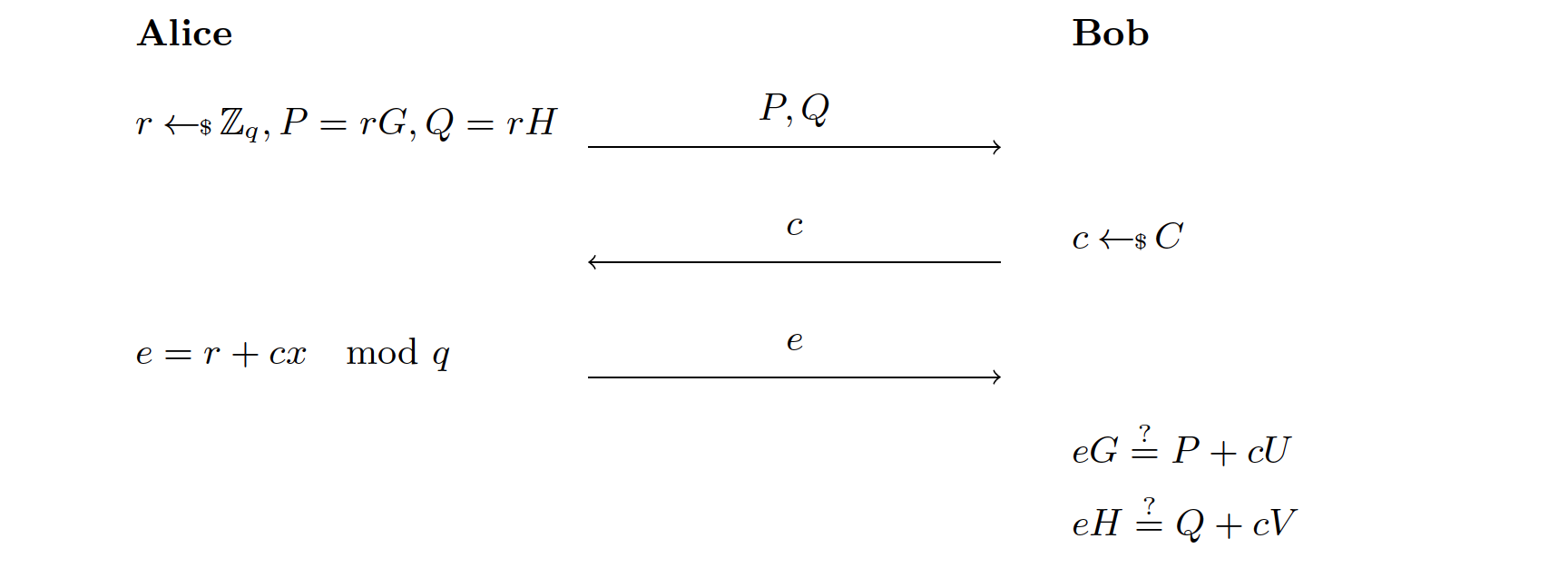
向 $cx$ 中加上随机数 $r \mod{q}$ 就把 $cx$ 完全掩盖住了，从而并没有向 Bob 泄漏任何 $x$ 的信息。

类似 Schnorr ID 协议，为了证明 Alice 知道 $x$，且 $x=\log_G{(U)}=\log_H{(V)}$，我们要等 Alice 生成 $r$ 之后再克隆她。在一个 Alice 中，她收到 $c$，发送 $e$，在另一个中，她收到 $c'$，发送 $e'$。我们就有：

$\begin{aligned} eG&=P+cU\\ e'G&=P+c'U\\ eH&=Q+cU\\ e'H&=Q+c'U \end{aligned}$

从而可以推出 $(e-e')/(c-c')G=U$，即 $x=(e'-e)/(c'-c)$，也可以推出 $(e-e')/(c-c')H=Q$，即 $x=(e'-e)/(c'-c)$，从而观察到两组方程可以得到同样的 $x$。

5 Fiat-Shamir heuristics 和非交互式零知识证明

在实践中，交互式协议有些缺点：他们很消耗带宽并需要各方都在线且相互同步。Fiat 和 Shamir 告诉我们，可以用 SHA256 这样的密码学哈希函数把交互式协议转化成非交互式协议。

5.1 Schnorr 签名

为了把 Shnorr 交互式 ID 协议转化为非交互式的，Alice 会使用一个密码学哈希函数来计算 $c=hash(R)$，而不是等 Bob 生成随机的 $c$ 了。

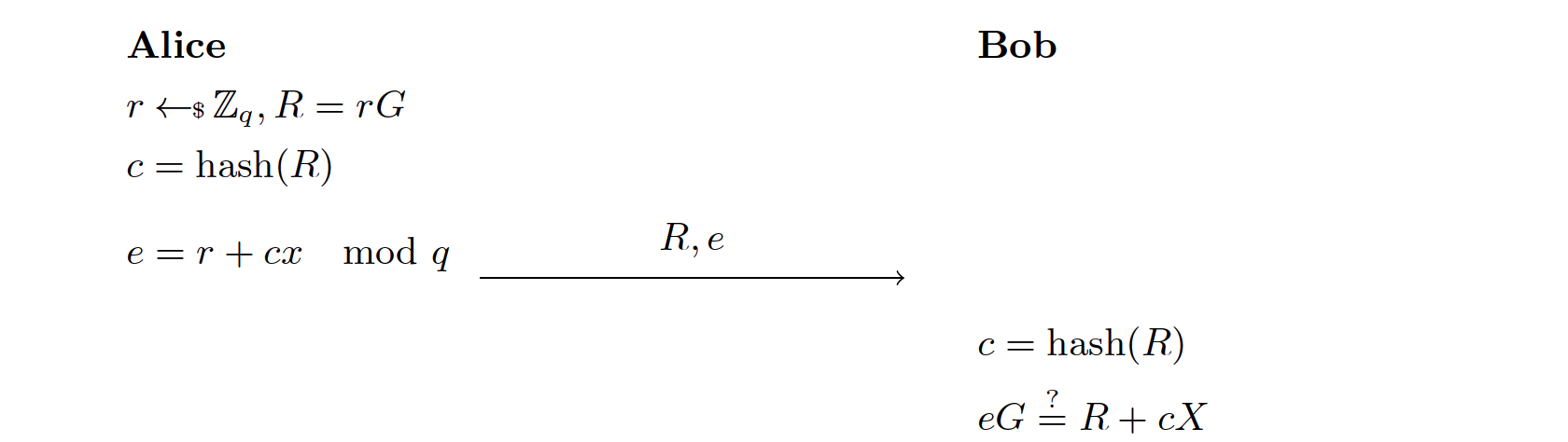
我们来研究一下为什么这个非交互式的协和和交互式的一样安全。在 Schnorr ID 协议一节中，我们注意到如果 Alice 可以提前预测 $c$，那么协议就不再安全了。Fiat-Shamir 转化有把协议变得不安全吗？答案是否定的，但是证明这点并不平凡。让我们回想一下密码学哈希的特性。对于密码学哈希函数来说，你无法同时控制输入和输出，如果你选定了输出，你就无法找到对应的输入使它在求了哈希之后的结果和这个输出相同。所以 Alice 不能事先选定 $c$ 并计算出一个 $R$ 使得 $hash(R)=c$。话句话说，Alice 必须要先生成 $R$，再计算 $c=hash(R)$。但是一旦 $R$ 确定下来了，输出的 $c=hash(R)$ 类似于随机数，是不在 Alice 的掌控之中的。这就保证了 Shnorr ID 协议的安全。总的来说，密码学操作的先后顺序对协议的安全性非常重要，所以要注意你的程序的状态机。

Schnorr 签名 [12] 是上述协议的一个小改动。为了给信息 $m$ 签名，相较于计算 $c=hash(R)$，我们计算 $c=hash(R||m)$，而签名就是 $(R,e=r+cx \mod{q})$。

5.2 非交互式 Chaum-Pedersen 协议

读完了上一节，你很容易想到 $c=hash(P,Q)$。值得一提的是，我们可以给哈希函数添加公共参数来提升协议的安全性。密码学哈希的目的是为了一起 blind 参数，所以在有些协议中你可能会看到类似于 $c=hash(G,H,U,V,P,Q)$。完整的协议如下：

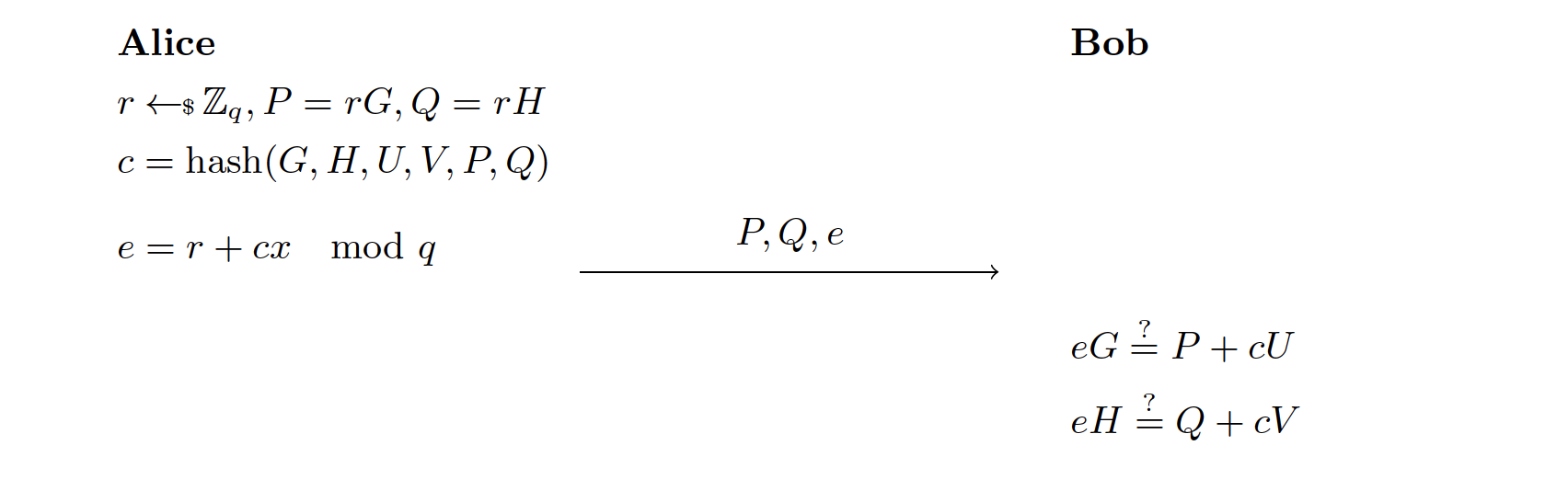
6 环签名

为了验证一个签名，验证者必须知道签名人的公钥。所以如果你在要发送的信息上使用例如 Schnorr 签名这样的数字签名，那么所有人都会知道签名的人是你。虽然这是预期的安全性质。但是有些时候你不想被追踪哪些东西是你签的，也不想承担相应的责任。环签名（ring signature）[13] 就允许签名人混入 $n$ 个用户之中，即，如果有 $n$ 个用户，他们中只有一个人签了名，签名并不会泄漏是谁，但是验证者可以验证是其中的一人签的。

我们会介绍一个基于 Schnorr 签名和 OR-proof 技术 [14] [15] 的协议。先来回忆一下，Schnorr 签名长这样：

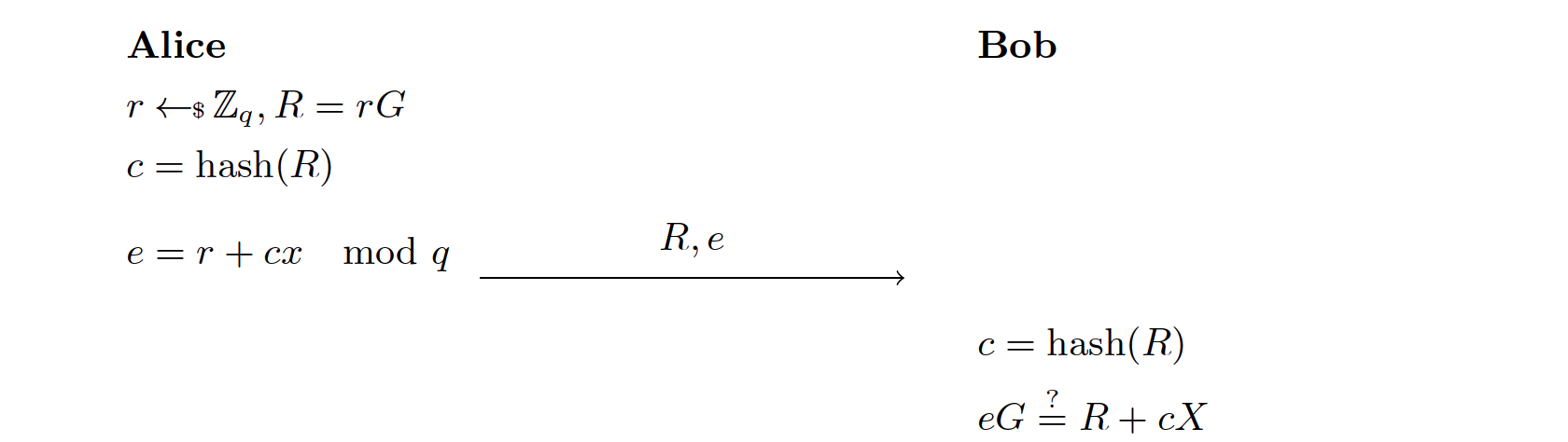
假设有 $n$ 个用户 $\text{user}_1,\dots, \text{user}_n$，其中 $\text{user}_i$ 是签名人。$\text{user}_i$ 用他的私钥 $x_i$ 正常给信息 $m$ 签名。然而，$\text{user}_j,j\ne i$ 不会使用自己的私钥，但是仍然要输出一个能通过验证的签名。你可能觉得这句话不明所以。的确，如果一个用户能不用自己的私钥生成签名，那么我们的签名机制里头肯定有漏洞。解决这个矛盾的方式是给 $\text{user}_j$ 多一点空间，让他能作弊。我们给 $\text{user}_j$ 的额外能力就是让他可以提前选择 $c_j$。具体来说，$\text{user}_j,j\ne i$ 先选择 $c_i$，随机生成一个 $e_j$，然后计算 $R_j=e_jG-c_jX_j$。这样的话 $e_jG_j\overset{?}{=}R_j+c_jX_j$ 还是能通过的。我们做了什么呢？ $\text{user}_j,j\ne i$ 不仅自己选择了 $c_j$，而且把计算顺序调整为了 $c_j\rightarrow e_j \rightarrow R_j$，而不是常规的 $R_j\rightarrow c_j \rightarrow e_j$。这一节再次强调，密码学操作的顺序是保证协议安全的重中之重，所以要紧盯程序的状态机。用上述技巧，$\text{user}_j$ 可以在不知道或者不使用密钥 $x_j$ 的情况下生成签名。

还差一点就要讲完了。我漏掉了一个重要的细节，$\text{user}_i$ 的 $c_i$ 是什么呢？退一步看，肯定会有什么类似于 Fiat-Shamir heuristic 中用哈希计算出来的 $c$。那么这个 $c$ 是怎么联系到 $c_i$ 和 $c_j,j\ne i$ 的呢？论文 [14] [15] 中给了一个很漂亮的解法：

$\text{user}_j,j\ne i$ 随机生成 $c_j$、$e_j$，并如上面所说的计算出 $R_j=e_jG-c_jX_j$。另一方面，$\text{user}_i$ 则随机生成 $r_i$，正常计算出 $R_i=r_iG$。$c$ 则由 $hash(m,R_1,\dots,R_n)$ 计算出，这把 $R_1,\dots,R_n$ 都绑到 $m$ 上了。一个技巧是用 $c_i=\oplus_{j\ne i}c_j\oplus c$，从而使 $c=c_1\oplus\dots\oplus c_n$。核心的想法是对于这样一个 $n$ 变量的方程，只有一个限制条件，因此验证者会强制 $n$ 个用户中有且只有 1 个选择（这里感觉翻的不太对...原文是 I.e., the verifier forces n users to have 1 and only 1 choice），从而对应了只有 1 个用户用自己的私钥对 $m$ 签了名，而其他的都是在作弊。最后，很显然验证者没法从所有的值中区分出 $c_i,e_i,R_i$，所以验证者不知道是 $\text{user}_i$ 是谁。

7 Shamir 密钥共享

“不要把鸡蛋放在一个篮子里”。在本节中，我们会谨遵这条至理名言来保护我们的密钥。

假设我们有一个需要保护的秘密 $s$。把 $s$ 存在一个系统里听起来不是一个好的策略。一个更好的方法是把 $s$ 分成几份然后存在不同的系统里。这样就增加了攻击的成本，因为攻击者需要攻击多个系统才能得到 $s$。我们会把 $s$ 分成 $n$ 份 $s_1, \dots, s_n$，并且其中的任意 $k$ 份都可以重构出 $s$，但是任意 $k-1$ 份不行。

令 $P(x)$ 为 $\mathbb{F}_p$ 上的 $k$ 阶多项式，即 $P(x)=a_{k-1}x^{k-1}+a_{k-2}x^{k-2}+\dots+a_0$，其中 $a_0, \dots,a_{k-1}\in\mathbb{F}_p$。我们会使用下面的这条多项式的性质：如果我们知道 $k$ 个不同的 $x_1, \dots, x_k$ 对应的值 $P(x_1), \dots, P(x_k)$，我们就可以重建出 $P(x)$（译者注，即求解出 $a_0, \dots, a_{k-1}$），但是仅仅知道 $k-1$ 个位置的 $P(x_i)$ 是不够的。为什么呢？让我们举一个小例子来说服自己。假如说 $k=2$，$P(x)=a_1x+a_0$。$(x,y=a_1x+a_0)$ 的图像就是一条直线。知道 2 个点 $(x_0,y_0=a_1x_0+a_0)$ 和 $(x_1,y_1=a_1x_1+a_0)$ 就可以确定下来这条线了，但是只知道一个点 $(x_0,y_0=a_1x_0+a_0)$ 就不行，因为经过这个点的直线有无数条。

运用上述的性质，Shamir 的协议 [16] 简单而优雅：设定 $a_0=s$，并随机生成 $a_1,\dots,a_{k-1}$，$n$ 个系统上保存的 $n$ 段数据分别是 $s_1=P(1),s_2=P(2),\dots,s_n=P(n)$，知道其中任意 $k$ 个 $s_i$ 就可以唯一确定 $P(x)$ 从而可以得到 $s=a_0=P(0)$，而只知道 $k-1$ 个则不行。

8 安全多方签名计算

假如说我们有一个私钥 $x$ 用来生成数字签名，根据漂亮的 Shamir 密钥共享协议，为了保护 $x$，我们需要把 $x$ 分成几段并把他们存在不同的系统里。我们的管理密钥的任务到这里的就做完了吗？如果我们仔细想想，会发现 Shamir 密钥共享在实践中有个问题。作为一个攻击者，我不关心 $x$ 被分成多份存在了不同的系统里，我只要等着 $x$ 在某个系统里被重建的时候再攻击那个系统就好了。

为了解决上述攻击，我们需要更强的安全要求。在把密钥 $x$ 分成 $x_1,\dots,x_n$ 并存在不同的系统里之后，这些系统只能使用自己的 $x_i$。我们会让这些系统交互，最后一起生成基于 $x$ 的签名，但是 $x_1,\dots,x_n$ 都保留在自己手上，即，他们不会向其他系统或其他人泄漏 $x_1,\dots,x_n$。在这样的设计下，攻击的开销就明显增长了，因为要获得 $x$ 就必须攻击整个系统。

8.1 安全多方 Schnorr 签名计算

下面考虑 $n=2$ 的特殊情况（对于 Schnorr 签名，很容易扩展到 $n$ 个系统）。安全的两方 Schnorr 签名非常直接。把 $x$ 分成 $x_1$、$x_2$ 从而使 $x=x_1+x_2\mod{q}$。类似地，我们要生成随机数 $r$ ，也分为 2 份，使得 $r=r_1+r_2 \mod{q}$。

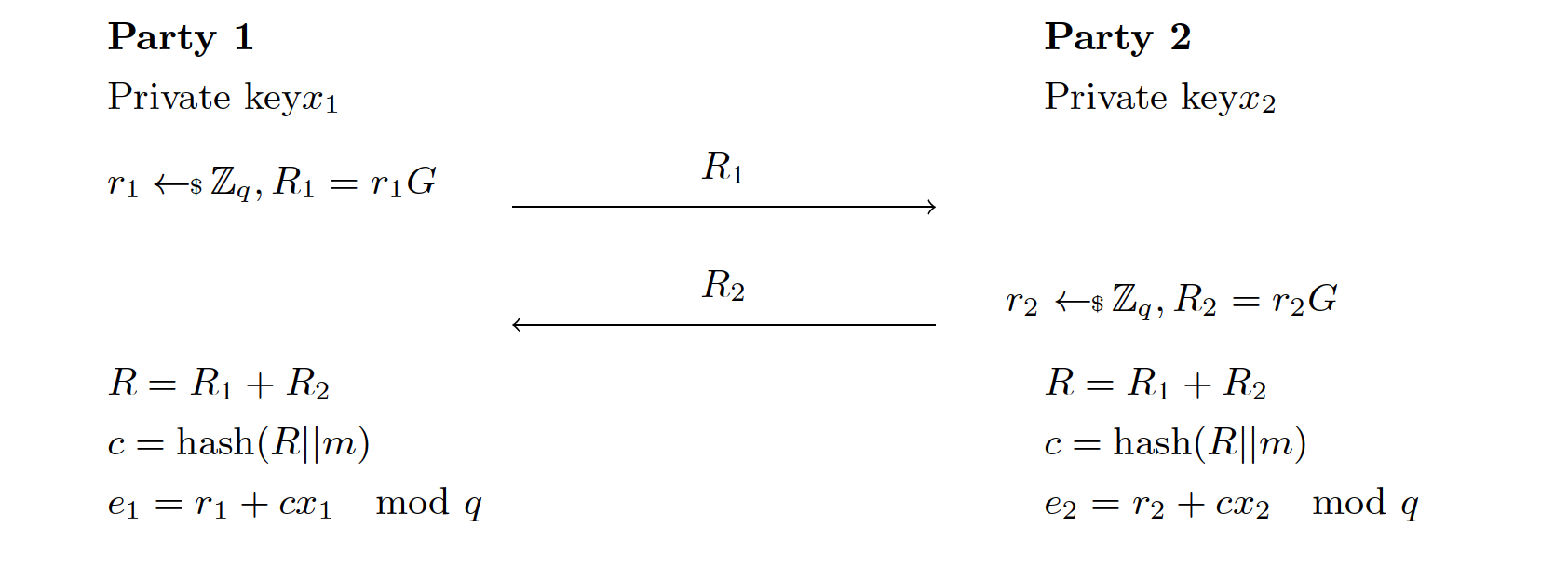
在上述协议中，双方分别计算了自己的 $R_1,R_2$ 并交换。$R$ 是 $R_1$ 与 $R_2$ 的和。双方还各自计算了 $c, e_1, e_2$。$m$ 的签名为 $R=R_1,R_2,e=e_1,e_2$。为什么呢？因为我们有：

$\begin{aligned} R&=R_1+R_2=r_1G+r_2G=(r_1+r_2)G=rG\\ e&=e_1+e_2=r_1+cx_1+r_2+cx_2=(r_1+r_2)+c(x_1+x_2)\\ &=r+cx\mod{q} \end{aligned}$

我们可以看到 $(R,e)$ 是有效的有 $x$ 进行的 $m$ 的签名。总结一下，各方都保护了自己的 $x_1,x_2$，在本地生成了签名，而总的签名是各方签名之和。

9 基于配对的密码学

如果你已经看到了这一节，那么你应该已经见到了很多基于椭圆曲线的协议了。我们所有的协议都是基于 1 条椭圆曲线的。然而，密码学家不愿意止步于此。他们想同时用 2 条曲线。这简直要把我逼疯了 :) 你知道一个像我一样不够厉害的安全工程师的生活有多悲惨吗？我不得不处理越来越困难的数学。在写完这篇文章之后，我要从密码学中退休。但是你，我的朋友，要用这些精彩的密码学协议来继续让世界变得更安全 :)

配对 [17] 的定义是一组映射 $e: E_1\times E_2\rightarrow F$，其中 $E_1, E_2$ 是一对椭圆曲线（根据协议不同，$E_1,E_2$ 可能相同），$F$ 是一个域，类似 $\mathbb{F}_{p^k}$。在我们继续之前，要注意到 $e$ 把两个椭圆曲线映射为一个域。我们稍后会看到这如何深远地影响了安全界。

我们使用的配对有一些很好的性质，例如：$e(P+Q, R)=e(P, R)e(Q, R)$ 以及 $e(aP, bQ)=e(P, Q)^{ab}$，这里 $a,b\in \mathbb{Z}$。一个理解数学的小技巧是去看它所包含的引申意义，所以让我们稍微研究研究这个公式。我们有：$e(aP,bQ)=e(P,Q)^{ab}=e(abP,Q)=e(P,Q)^{ab}=e(bP,aQ)$。我们做到了在两个曲线之间移动“系数”但依然保证映射的值等于 $e(P,Q)^{ab}$。在基于配对的密码学中，这个技巧被不断使用。由这里得来的一个很酷的结论是：当 $E_1=E_2=E$ 且 $P=Q=G$ 为椭圆曲线 $E$ 的基点时，我们有 $e(aG,bG)=e(G,G)^{ab}=e(abG,G)$。即，给定 $G,aG,bG$ 我们可以区分一个点是 $abG$ 还是随机点，因为我们知道 $e(abG,G)=e(aG,bG)$，而 $e(\text{random number},G)\ne e(aG,bG)$。换句话说，一旦我们有了配对，decisional Diffie-Hellman (DDH) 问题变得很简单了！

9.1 MOV 攻击

如果一个椭圆曲线有配对，Menezes、Okamoto 和 Vanstone（MOV）[18] 发明了一种很漂亮的针对椭圆曲线离散对数问题的攻击。回想一下，椭圆曲线的离散对数问题是指，对于椭圆曲线 $E$ 和基点 $G$ 以及点 $A$，找到满足 $A=aG$ 的 $a$。

攻击是这样的：假设 $B$ 是 $E$ 上一个可以与 $A$ 配对的点。我们有 $e(A,B)=e(aG,B)=e(G,B)^a$。注意到 $e(A,B)$ 和 $e(G,B)$ 均属于 $F$。所以我们可以把椭圆曲线上的离散对数问题转化为域上的问题：给定 $u=e(G,B)$ 和 $v=e(A,B)$，找到 $a$ 使得 $v=u^a$。总的来说，域上的离散对数问题比椭圆曲线上的要好解决，所以任何使用有配对的椭圆曲线的系统的安全性都下降了。我不是说你不该使用配对，只是要小心这带来的风险。天下没有免费的午餐。

9.2 BLS 签名

在 2001 年，Boneh、Lynn 和 Shacham（BLS）[19] 提出了一个很酷的基于配对的签名机制。假设 Alice 有密钥 $x$，她的公钥是 $X=xG$，$H$ 是一个哈希函数，可以将信息映射到椭圆曲线 $E$ 上。签名仅仅是 $\sigma=xH(m)$。为了验证签名 $\sigma$，我们需要检查是否有 $e(\sigma, G)\overset{?}{=}e(H(m), X)$ 。为什么呢？因为有 $e(\sigma, G)=e(xH(m),G)=e(H(m),G)^x=e(H(m), xG)=e(H(m),X)$。

9.3 BLS 签名聚合

传统上讲，BLS 的吸引力是它很短。然而，随着对域上离散对数问题的密码分析（cryptanalysis）的进展，密码学家需要增加安全参数和签名大小来达到合适的安全等级。另一方面来说，这个签名机制有一个至今仍适用的很好的性质，他允许签名聚合（signature aggregation）[20]。

签名聚合的基本目标是这样的，假设我们有 $n$ 个用户，每人都有私钥 $x_i$，公钥 $X_i=x_iG$。每个用户都给自己的信息 $m_i$ 签名，得到 $\sigma_i=x_iH(m_i)$。下面，为了做验证，相较于单独对每个 $\sigma_i$ 做验证，我们想直接验证一个聚合了的签名。这不仅可以减少 CPU 计算周期，也可以节省传输签名的带宽。

为了达到这一目标，我们会这样计算聚合签名 $\sigma$：$\sigma=\sigma_1+\dots+\sigma_n$。可以通过 $e(\sigma,G)\overset{?}{=}e(H(m_1),X_1)\dots(H(m_n),X_n)$ 来验证 $\sigma$。因为我们有：

$\begin{aligned} e(\sigma,G)&=e(\sigma_1+\dots+\sigma_n,G)\\ &=e(x_1H(m_1)+\dots+x_nH(m_n),G)\\ &=e(x_1H(m_1),G)\dots(x_nH(m_n),G)\\ &=e(H(m_1),G)^{x_1}\dots(H(m_n),G)^{x_n}\\ &=e(H(m_1),x_1G)\dots(H(m_n),x_nG)\\ &=e(H(m_1),X_1)\dots(H(m_n),X_n) \end{aligned}$

10 盲签名

1983 年，当电子支付还处于早期，有个叫 David Chanum 的厉害的人就开始担心用户被银行追踪，所以他发明了极具未来感的盲签名（blind signature）。让我们向 David Chanum 致敬。

考虑如下的场景。假设银行有私钥 $x$，与来自椭圆曲线 $E$ 的公钥 $X=xG$。银行只发行固定面值的 token，例如 $1。一个 token 是一个序列号以及对应的银行签名，用户可以拿着它到商店。商店可以用银行的公钥 $X$ 来验证银行的签名。

这个协议有啥问题吗？用户可以在不同的商店复用有同一个序列号的同一个 token。这被称为双重支付（double-spending attack）。为了解决这个问题，商店需要联系银行来确保每个序列号只能用一次。银行则要有一个数据库来保存所有用过的序列号。这样的结果是，银行知道用户在哪些商店用过他们的 token，从而可以定位用户的支付地点和支付时间。

为了保护用户隐私，我们需要让用户选择他们的序列号，把他们摘出去，而银行仍可以给他们签名。令 $m$ 为需要签名的信息/序列号，我们会描述一个基于 Alexandra Boldyreva 提出的 BLS 签名 [22] 的盲签名。回忆一下，在 BLS 中，$m$ 的签名就是 $xH(m)$。

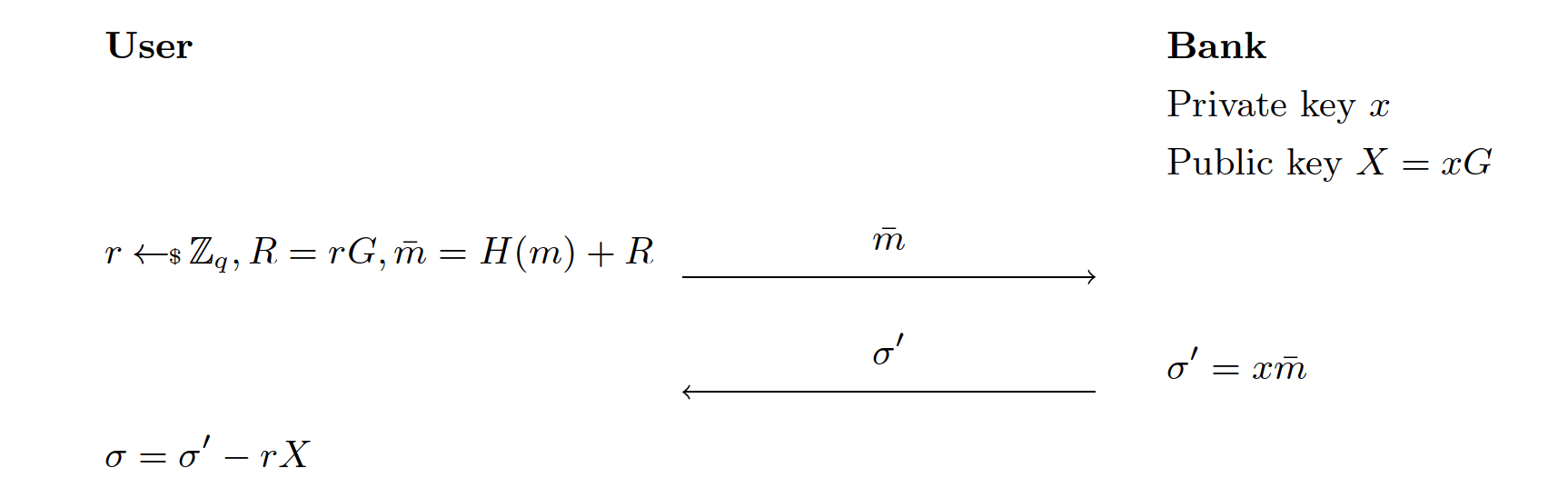
在上图的协议中，银行知道 $\bar{m}$，但是对 $m$ 一无所知，因为向 $H(m)$ 中加了随机点 $R$ 把原来的值遮住了。银行通过 $\sigma'=x\bar{m}$ 对 $\bar{m}=H(m)+R$ 签名。用户则可以用这样的方式来提取出 $m$ 的签名：$\sigma'-rX=x(H(m)+rG)-rxG=xH(m)=\sigma$。

11. 不经意传输

让我们来了解一下基于椭圆曲线 Diffie-Hellman 协议 [23] 的一个简单的不经意传输（oblivious transfer OT）协议。要解决的问题是这样的：Alice 有 2 条信息 $m_0$ 和 $m_1$，Bob 选择一个随机位 $c$（即 $c$ 等于 0 或 1）。目标是让 Bob 在收到 $m_c$ 的情况下，对 $m_{1-c}$ 完全不知情。

你找到这个协议了吗？很简单：Bob 把 $c$ 发给 Alice，然后 Alice 把 $m_c$ 发送回来就行了 :) 我在问题叙述里故意漏掉了一条重要的安全性质：Alice 不能知道 $c$ 的值。现在，这个问题变得极具挑战。在读题的时候要仔细哦！

让我们回忆一下 Diffie-Hellman 协议。注意在最后一步，我们会用 $k$ 去加密 Alice 的信息 $m_0,m_1$。

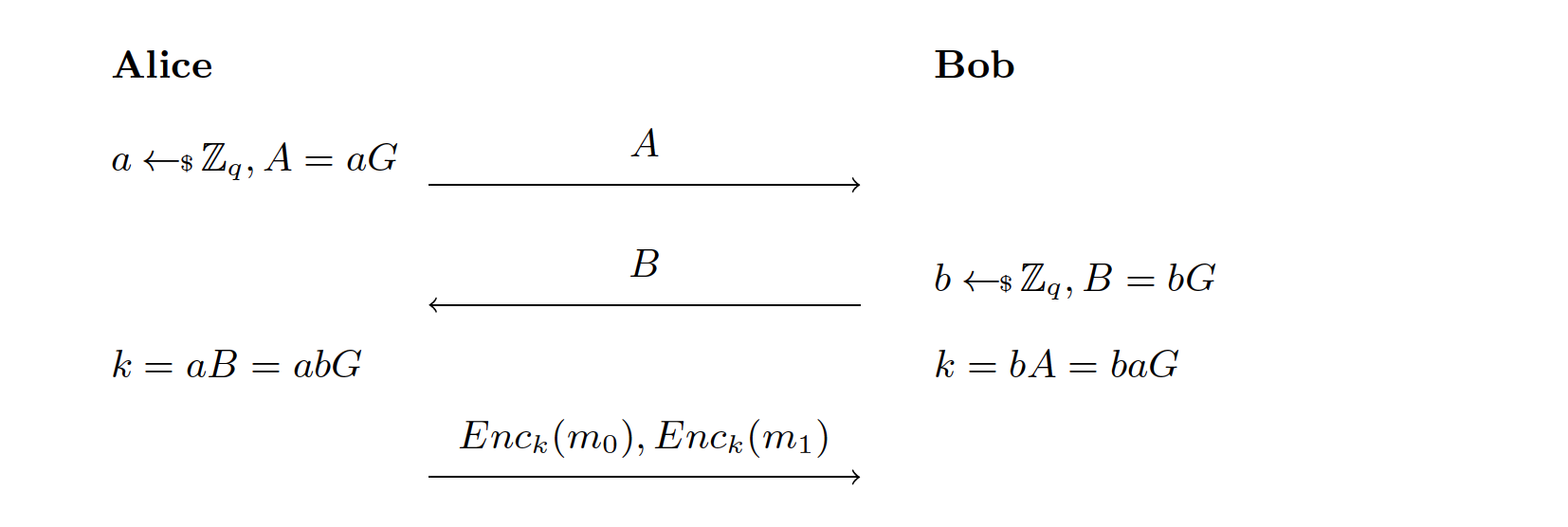
在这种基本的 ECDH 中，Bob 可以同时解码 $Enc_k(m_0), Enc_k(m_1)$。所以需要用的技巧是当 $c=0$，Bob 发送他自己的公钥 $B=bG$，当 $c=1$ 时，Bob 发送 $B=bG+A$。Alice 没法区分这两种情况，因为对于她来说，$bG$ 和 $bG+A$ 看起来都像是随机值。收到 Bob 的信息之后，Alice 的任务是让 Bob 只能解码其中的一条信息。所以 Alice 生成 2 个密钥：$k_0=aB$ 和 $k_1=aB-aA$，并发给 Bob $Enc_{k_0}(m_0)$ 和 $Enc_{k_1}(m_1)$。可以看出，2 个密钥中只有 1 个是被共享了的，而另一个对于 Bob 来说是随机数。

如果 $c=0, B=bG$，那么 $k_0=aB=abG$ 是共享密钥，而 $k_1=a(B-A)=abG-aA$ 对于 Bob 来说是个随机数，因为 Bob 不知道 $aA$ 的值。

而如果 $c=1, B=bG+A$，那么 $k_1=a(B-A)=abG$ 是共享密钥，而 $k_0=aB=abG+aA$ 对于 Bob 来说是个随机数，因为 Bob 不知道 $aA$ 的值。

整理一下，Bob 只能知道 $k_c$，所以也就只能解密 $Enc_{k_0}(m_0),Enc_{k_1}(m_1)$ 中的一条从而得到 $m_c$。问题解决了。

12. 承诺机制

你有没有承诺过自己会把这篇文章读完？你有过，对吧？不过即使你说你做过这样的承诺，我也不相信，因为你很容易就可以找个借口从而不履行它。在本节，我们会看看密码学承诺机制，它会让人无法不履行承诺。

承诺机制常由 2 部分组成。在承诺阶段（commit phase），承诺人 Alice 会承诺一个值，但是隐藏它。在公开阶段（reveal phase），Alice 会展示承诺的值，我们则会保证 Alice 无法拿一个别的值来骗我们。

12.1 基于哈希的承诺机制

取一个密码学哈希函数（例如 SHA256），为了承诺一个值，Alice 随机生成一个定长大数 $r$（如 128 位），并公布 $c=h(r||v)$。在公开承诺值的时候，Alice 公开 $r$ 和 $v$，其他人则可以通过 $h(r||v) \overset{?}{=} c$ 来验证。

为什么不直接用 $c=h(v)$ 呢？这样的问题是可能会泄漏 $v$，因为攻击者可以用暴力搜索，不断计算 $h(v)$ 并和 $c$ 比较来找到 $v$。$r$ 会提升随机性，从而让攻击者不可能猜出 $r||v$。

为什么 Alice 不能用别的值来作弊呢？如果要公开一个不同的值 $v'$，Alice 需要找到 $v'$、$r'$ 使得 $h(r'||v')=c=h(r||v)$。换句话说，Alice 需要给 $h$ 找一个碰撞。对于 SHA256 这样的标准密码学哈希函数，这是做不到的。

12.2 Pedersen 承诺机制

Pedersen 承诺机制 [24] 基于离散对数问题，即对于椭圆曲线 $E$ 上的两个点 $G$ 和 $H$，无法计算出 $\log_G{(H)}$。为了承诺值 $v$，Alice 会生成一个随机值 $r$，并发布 $c=vG+rH$。为了公开承诺，Alice 会公开 $r$ 和 $v$。

为什么不能从 $c$ 推出 $v$ 呢？原因是 $rH$ 是 $E$ 上的随机点，所以不管 $vG$ 是多少，加上 $rH$ 之后就完全把这个值隐藏起来了。

为什么 Alice 不能作弊呢？为了作弊 Alice 需要找到 $v'$、$r'$ 使得 $c=vG+rH=v'G+r'G$。也就是 $(v-v')G=(r-r')H$，即 $(v-v')/(r-r')G=H$。那相当于 Alice 算出了 $\log_G{(H)}=(v-v')/(r-r')$。这和我们上面的假设相悖了。换句话说，如果你不相信没人能知道 $\log_G{(H)}$ 是多少，就不要用 Pedersen 承诺机制，因为如果知道了这个值就可能会作弊。

12.2.1 同态性质

Pedersen 承诺机制有一个很好的同态性质：给定 2 个承诺 $c_1$、$c_2$，即使我们不知道他们的承诺值，我们可以计算出另一个承诺 $c=c_1+c_2$ 对应了两个承诺值的和。可以很直接地验证这点：如果 $c_1=v_1G+r_1H, c_2=v_2G+r_2H$，其中 $v_1$、$v_2$ 分别是两个承诺值，那么 $c=c_1 + c_2=(v_1+v_2)G+(r_1+r_2)H$ 对应的承诺值是 $v=v_1+v_2$。

13. 格密码学

最近 10 年里，格密码学（lattice based cryptography）[25, 4] 蓬勃发展。主要有 2 个原因。第一个原因是格密码学在使用量子计算机的情况下是安全的，而 ECDH 密钥交换和 RSA 不是。因为量子计算机比传统计算机更强大，我们能推出格密码学比在传统计算机上更安全吗？并不行，因为我们最初的安全假设（注意是假设不是事实）可能是错的。就像密码学中的其他很多东西，格密码学的安全性仅仅是一个假设，没人知道是不是对的。另外，没有证据表明格密码学在传统计算机上比 ECDH 更安全。因此，径直冲进格密码学而抛弃 ECDH 这样的经典协议是不明智的。第二个原因是格密码学让密码学家可以设计很多有超凡特性的协议，这是之前做不到的。一个著名的格密码学的应用就是全同态加密（full homomorphic encryption, FHE）。

我们会在不定义格是什么的情况下描述格密码学，因为这其中的数据已经远超我的能力范围了。我们会转而讨论一些拥有格结构的多项式，这样就比较熟悉了。顺便，你有注意到本文的一个特点吗？每当我看到一个复杂的东西的时候，我都会掉头跑路，因为实在是处理不了这些复杂的东西！

格密码学常常依赖于的是找到一些小（small）的东西或者有误差（error）地求解方程的难度很高。所以每次你在多项式里看到小或者误差，你就知道自己已经踏入格密码学的领地了。本节中，我们会处理 $\mathbb{Z}_q[x]/(P(x))$ 或者 $\mathbb{Z}[x]/(P(x))$ 中的多项式，即系数在 $\mathbb{Z}_q$（或 $\mathbb{Z}$ ）中的多项式，他们的操作都要 $\mod{P(x)}$。对于 $\mathbb{Z}_q[x]/(P(x))$ 中的多项式有 2 个很难解的问题。我们会简单介绍一下他们，主要是为了引出一些术语，并给你一个粗略的概念我们是在依赖着什么样的难问题。

第一个问题是 Ring-Short Integer Solution (R-SIS)：给定 $\mathbb{Z}_q[x]/(P(x))$ 中 $m$ 个多项式 $a_i$，找到 $\mathbb{Z}_q[x]/(P(x))$ 中 $m$ 个小多项式 $z_i$ ，使得 $\sum_i{a_i.z_i}=0$。注意没有“小”这个要求，问题就很好解了。

第二个问题叫 Ring-Learning With Error (R-LWE)：给定 $\mathbb{Z}_q[x]/(P(x))$ 中的私钥 $s$， $\mathbb{Z}_q[x]/(P(x))$ 中 $m$ 个随机多项式 $a_i$ 和 $m$ 个“误差”多项式 $e_i$，区分 $(a_i,b_i=a_i.s+e_i)$ 和随机多项式对。注意没有“误差”的话，这个问题也是平凡的。

13.1 格密码学同态加密

假设我们要把数据存在云上。为了保护数据，我们会事先把他们加密并保存好密钥。另一方面，我们希望利用好云上的算力，所以想让云在不知道明文是什么的情况下对密文进行些计算。同态加密就是一种能够完成这一目标的特殊加密方法。本节中，我们会介绍一个简单的基于格密码学的同态加密 [26]。

我们会使用 $\mathbb{Z}_q[x]/(x^{2^k}+1)$（$q$ 为质数），即，系数在 $\mathbb{Z}_q$ 中的多项式，运算都要 $\mod{x^{2^k}+1}$。我们还会用一个远小于 $q$ 的模（modulus）$t$。注意，本节的所有东西，密钥、信息、密文都是多项式。

私钥 $s$ 是 $\mathbb{Z}_q[x]/(x^{2^k}+1)$ 上的多项式。

为了加密消息多项式 $m\in\mathbb{Z}_q[x]/(x^{2^k}+1)$，我们随机生成一个多项式 $a$，一个小的误差多项式 $e$ 。密文就是 $c=Enc(m)=(c_0,c_1)=(-a,as+m+et)$。

解密的方式是计算 $c_1+c_0s \mod{t}=as+m+et-as \mod{t}=m+et\mod{t}=m$。

验证一下这种加密满足加法同态，如果我们把 $m$ 和 $m'$ 的加密结果，$c=Enc(m)=(c_0,c_1)=(-a,as+m+et)$ 和 $c'=Enc(m')=(c_0',c_1')=(-a',a's+m'+e't)$ 相加，就会得到：

$\begin{aligned} (c_0,c_1)+(c_0',c_1')&=(c_0+c_0',c_1+c_1')\\ &=(-a-a',as+m+et+a's+m'+e't)\\ &=(-(a+a'),(a+a')s+(m+m')+(e+e')t) \end{aligned}$

如果我们定义 $a''=a+a',m''=m+m',e''=e+e'$，就有：$c''=(c_0'',c_1'')=(c_0,c_1)+(c_0',c_1')$ 是用误差 $e''=e+e'$ 对 $m''=m+m'$ 的加密。也就是说，我们在不知道信息内容的情况下对密文进行相加，得到的结果就是信息之和。是不是很酷？

另一个很好的性质在于，如果你在 $m$ 的加密结果上乘一个多项式 $p$，那么结果就是 $pm$ 的密文。我们还是来具体推导一下，假如说 $m$ 的加密结果为 $(c_0,c_1)=(-a,as+m+et)$，我们有：

$\begin{aligned} p(c_0,c_1)&=(pc_0,pc_1)\\ &=(p(-a),p(as+m+et))\\ &=(-pa,pas+pm+pet) \end{aligned}$

如果我们定义 $a'=pa,m'=pm,e'=pe$，我们就有 $(c_0',c_1')=p(c_0,c_1)$ 是用误差 $e'=pe$ 对 $m'=pm$ 的加密。

最后要说的一点是，在两个例子中，误差都扩大了。格密码学要求误差保持很小，所以已经提出了很多逐步减小误差的方法。我们不在这里讨论减少误差的技术了，还是来看看上面提到的同态加密的一个超棒的应用吧。

13.2 隐私信息提取

假如说服务器里有个公开数据集（例如，存了电影、歌曲、歌词、故事、书籍）里面有 $n$ 条数据 $x_1,\dots,x_n$。用户想从数据库查看 $x_i$，但是不想泄漏给服务器他下载了哪条数据。这是为了保护用户隐私。一个明显的方法是用户直接下载全部 $n$ 条数据，隐私保护得非常好，但是很消耗带宽和用户本地的存储空间。我们希望利用同态加密 [27] 来用 CPU 换带宽与存储。一个基本的协议如下：

用户配置一个 0、1 序列，其中只有 $i$ 处为 1，其他处均为 0：$0,\dots,0,\underbrace{1}_{\text{index i}},0,\dots,0$，之后用同态加密这个序列，得到 $c_1=Enc(0),\dots,c_{i-1}=Enc(0),c_i=Enc(1),c_{i+1}=Enc(0),\dots,c_n=Enc(0)$。用户会把 $c_1,\dots,c_n$ 发送给服务器。

服务器计算 $x=x_1c_1+\dots+x_nc_n$，但是不知道 $i$ 是啥，并把结果 $x$ 发送回用户。

用户解密 $x$，得到 $x_i$。为什么呢？因为由同态性质，$x=x_1c_1+\dots+x_nc_n$ 和 $x_1.0+\dots+x_{i-1}.0+x_i.1+x_{i+1}.0+\dots+x_n.0$ 的密文是一样的。

14. 结论

想不到你真的看完了本文。你的耐心领我钦佩，谢谢！不过如果你是直接跳过来看结论的，还是麻烦你回去看看这篇文章 :)

我希望你可以在被高等密码学协议的难度吓跑之前感受到他们的美。而且幸运的话，你可能会在你的应用场景中使用这些绝妙的密码学协议。在那种情况下，不要忘了去看看很棒的密码学博客 [28] 以及关于应用密码学协议的严肃书籍 [14]。另一方面，如果你看到了这里还是对密码学协议一头雾水的话，那显然我写的很失败 :( 我会下次努力的 :)

引用文献

[1] Victor Shoup. A Computational Introduction to Number Theory and Algebra.

[2] Thomas W. Judson. Abstract Algebra: Theory and Applications.

[3] Lawrence C. Washington. Elliptic Curves: Number Theory and Cryptography.

[4] Chris Peikert. A decade of lattice cryptography.

[5] Peter Shor. Algorithms for quantum computation: discrete logarithms and factoring.

[6] Lov K. Grover. A fast quantum mechanical algorithm for database search.

[7] Whiteld Die and Martin E. Hellman. New directions in cryptography.

[8] Taher ElGamal. A public key cryptosystem and signature scheme based on discrete logarithms.

[9] Neal Koblitz. Elliptic curve cryptosystems.

[10] C.P. Schnorr. Ecient signature generation by smart cards.

[11] David Chaum and Torben Pryds Pedersen. Wallet databases with observers.

[12] C.P. Schnorr. Ecient signature generation by smart cards.

[13] Ronald L. Rivest, Adi Shamir, , and Yael Tauman. How to leak a secret.

[14] Dan Boneh and Victor Shoup. A Graduate Course in Applied Cryptography.

[15] Ronald Cramer, Ivan Damgard, and Berry Schoenmakers. Proofs of partial knowledge and simplied design of witness hiding protocols.

[16] Adi Shamir. How to share a secret.

[17] Ben Lynn. https://crypto.stanford.edu/pbc/notes/elliptic/.

[18] Afred Menezes, Scott Vanstone, and Tatsuaki Okamoto. Reducing elliptic curve logarithms to logarithms in a nite eld.

[19] Dan Boneh, Ben Lynn, and Hovav Shacham. Short signatures from the weil pairing.

[20] Dan Boneh, Craig Gentry, Ben Lynn, and Hovav Shacham. Aggregate and veriably encrypted signatures from bilinear maps.

[21] David Chaum. Blind signatures for untraceable payments.

[22] Alexandra Boldyreva. Threshold signatures, multisignatures and blind signatures based on the gap-die-hellman-group signature scheme.

[23] Tung Chou and Claudio Orlandi. The simplest protocol for oblivious transfer.

[24] Torben Pryds Pedersen. Non-interactive and information-theoretic secure veriable secret sharing.

[25] The 2nd biu winter school. https://cyber.biu.ac.il/event/the-2nd-biu-winter-school/.

[26] Simple homomorphic encryption library with lattices (shell) (https://github.com/google/shell-encryption).

[27] Carlos Aguilar-Melchor, Joris Barrier, Laurent Fousse, and Marc-Olivier Killijian. Xpir : Private information retrieval for everyone.

[28] Matthew Green. A few thoughts on cryptographic engineering (https://blog.cryptographyengineering.com/).